What is the arclength of #f(t) = (t-7,t+7)# on #t in [1,3]#?
1 Answer
Explanation:
The Arc Length for a Parametric Curve is given by
# L=int_alpha^beta sqrt((dx/dt)^2+(dy/dt)^2) \ dt #
So in this problem we have (using the product rule):
# x= t-7 => dx/dt = 1#
# y= t+7 => dy/dt = 1 #
So the Arc Length is;
# L= int_1^3 sqrt( (1)^2 + (1)^2) \ dt #
# \ \ = int_1^3 sqrt( 2 ) \ dt #
# \ \ = sqrt( 2 ) int_1^3 \ dt #
# \ \ = sqrt( 2 ) [t]_1^3 #
# \ \ = sqrt( 2 ) (3-1) #
# \ \ = 2sqrt( 2 ) #
Additionally, If we look at the actual graph of the parametric curve:
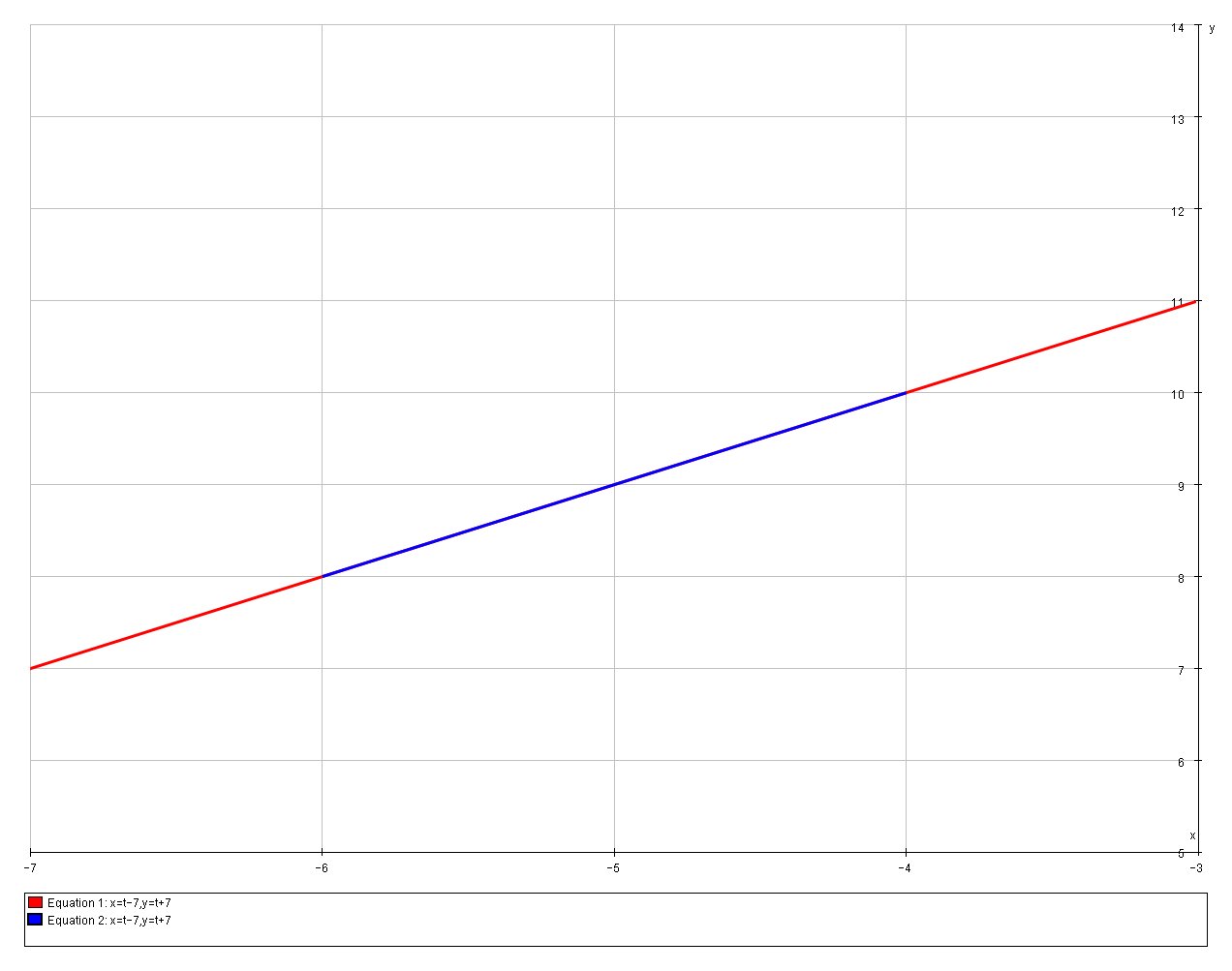
we can see that the equations represent a straight line, so in fact we can easily calculate the are length (coloured blue) from a triangle using Pythagoras:
#L=sqrt((-6-(-4))^2 + (10-8)^2) #
# \ \ \=sqrt(4+4) #
# \ \ \=sqrt(8) #
# \ \ \=2sqrt(2) # , as above
So, Maths Works!

