What is the area of a hexagon where all sides are 8 cm?
1 Answer
Area
Explanation:
A hexagon can be divided into
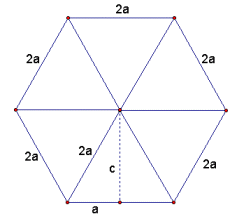 http://mathcentral.uregina.ca/QQ/database/QQ.02.06/trevor1.html
http://mathcentral.uregina.ca/QQ/database/QQ.02.06/trevor1.html
Using the Pythagorean theorem, we can solve for the height of the triangle:
#a^2+b^2=c^2#
where:
a = height
b = base
c = hypotenuse
Substitute your known values to find the height of the right triangle:
#a^2+b^2=c^2#
#a^2+(4)^2=(8)^2#
#a^2+16=64#
#a^2=64-16#
#a^2=48#
#a=sqrt(48)#
#a=4sqrt(3)#
Using the height of the triangle, we can substitute the value into the formula for area of a triangle to find the area of the equilateral triangle:
#Area_"triangle"=(base*height)/2#
#Area_"triangle"=((8)*(4sqrt(3)))/2#
#Area_"triangle"=(32sqrt(3))/2#
#Area_"triangle"=(2(16sqrt(3)))/(2(1))#
#Area_"triangle"=(color(red)cancelcolor(black)(2) (16sqrt(3)))/(color(red)cancelcolor(black)(2)(1))#
#Area_"triangle"=16sqrt(3)#
Now that we have found the area for
#Area_"hexagon"=6*(16sqrt(3))#
#Area_"hexagon"=96sqrt(3)#

