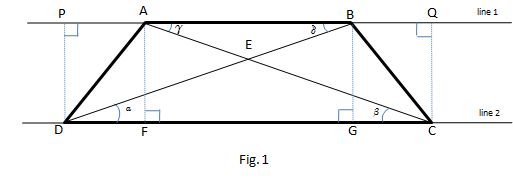
Consider Figure 1
![I have created this figure using MS Excel]
( )
)
In a trapezoid ABCD that satisfies the conditions of the problem (where BD=AC=30, DP=18, and AB is parallel to CD) we notice, applying the Alternate Interior Angles Theorem, that alpha=delta and beta=gamma.
If we draw two lines perpendicular to segment AB, forming segments AF and BG, we can see that triangle_(AFC)-=triangle_(BDG) (because both triangles are right ones and we know that the hypotenuse of one is equal to the hypotenuse of the other and that a leg of one triangle is equal to a leg of the other triangle) then alpha=beta => gamma=delta.
Since gamma=delta we can see that triangle_(ABD)-=triangle_(ABC) and AD=BC, therefore the trapezoid is isosceles.
We also can see that triangle_(ADP)-=triangle_(BCQ) => AP=BQ (or x=y in figure 2).
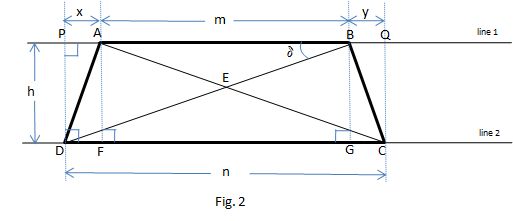
Consider Figure 2
![I have created this figure using MS Excel]
( )
)
We can see that the trapezoid in figure 2 has a different shape than the one in figure 1, but both satisfy the conditions of the problem. I presented this two figures to show that the information of the problem doesn't allow to determine the sizes of the base 1 (m) and of the base 2 (n) of the trapezoid, but we'll see that there's no need of more information to calculate the trapezoid's area.
In triangle_(BDP)
DB^2=DP^2+BP^2 => 30^2=18^2+(x+m)^2 => (x+m)^2=900-324=576 => x+m=24
Since n=m+x+y and x=y => n=m+2*x and m+n=m+m+2*x=2*(x+m)=2*24 => m+n=48
S_(trapezoid)=(base_1+base_2)/2*height=(m+n)/2*18=(48*18)/2=432
Note: we could try to determinate m and n conjugating these two equations:
In triangle_(ADP) -> AD^2=AP^2+h^2 => AD^2=(24-m)^2+18^2
In triangle_(ABD) -> AD^2=AB^2+BD^2-2*AB*BD*cos delta => AD^2=m^2+30^2-2*m*30*(4/5)
(cos delta =4/5 because sin delta = 18/30=3/5)
But resolving this system of two equations, we would only discover that m and the side AD are indeterminate.
 )
)  )
) 
