What is the area of the annulus shown in the diagram, given that the length of AB is 14cm?
We know that the formula for the area of an annulus is pi(R^2-r^2) .
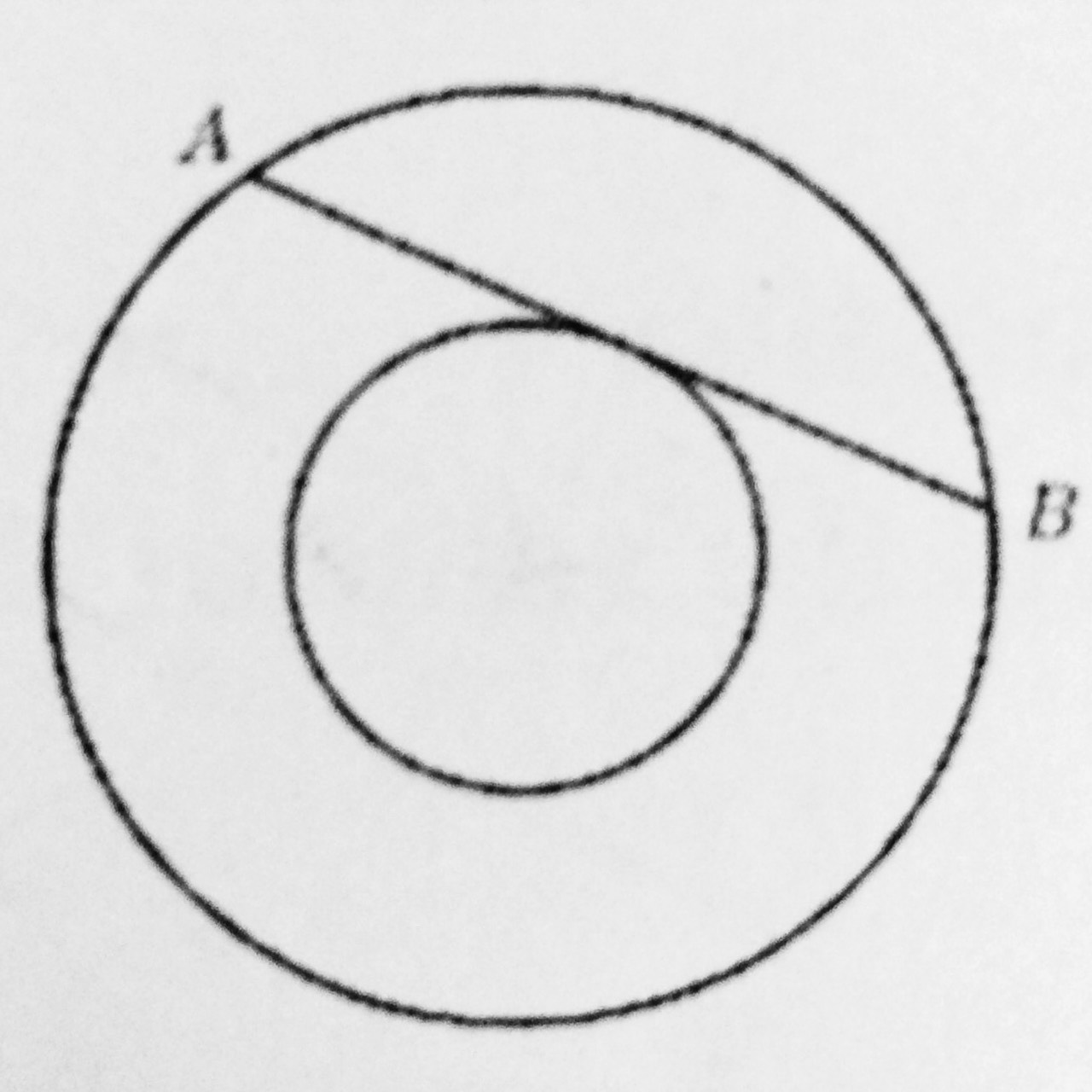
We know that the formula for the area of an annulus is

2 Answers
Nov 18, 2017
Explanation:
Nov 18, 2017
Explanation:
I assume that the two circles are concentric and
Let
As
as
by Pythagorean theorem,
Area of the annulus = shaded area

