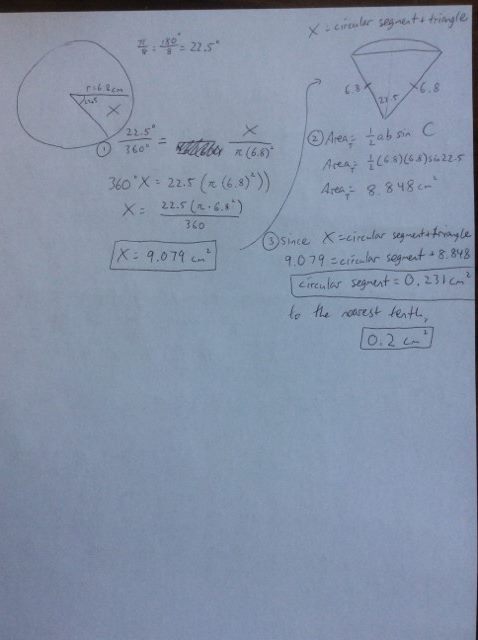
What is the area of the circular segment (to the nearest tenth) of a circle of radius 6.8 cm that subtends a central angle of #pi/8#?
1 Answer
We know that the central angle is
For simplicity, we converted this into degrees as
Here comes the important part:
The measure of the central angle is PROPORTIONAL to the area of the sector that the angle subtends.
Therefore, we can set up the proportion in equation (1):
Part divided by whole is equal to part divided by whole.
By that method, we can find the sector that
Now, we must dissect the sector.
We can separate the sector as a triangle and the circular segment that we want to find.
What do we know about the triangle? Hint: what do you notice about the legs?
That's right, both legs are radii, so they are both
Now, we have the area of the sector and the area of the triangle.
By equation (3), if we subtract the area of the triangle FROM the area of the sector, we will get the desired circular segment.