What is the area of the figure?
given by x=cos^3(t), y=sin^3(t), 0<=t<=2pi
given by
2 Answers
Please see below
Explanation:
I don't know if it's correct. Being a student this is all what I can do(atleast for now)
also,
similarly,
now integrate to find the equation and thus the graph
putting different values of K will give the graph
graph{x/(x^(2/3)-1)^(3/2) [-10, 10, -5, 5]}
We need to integrate as
Explanation:
When you have a parametric set of equations and want to find the area under the curve, we need to define a function relative to
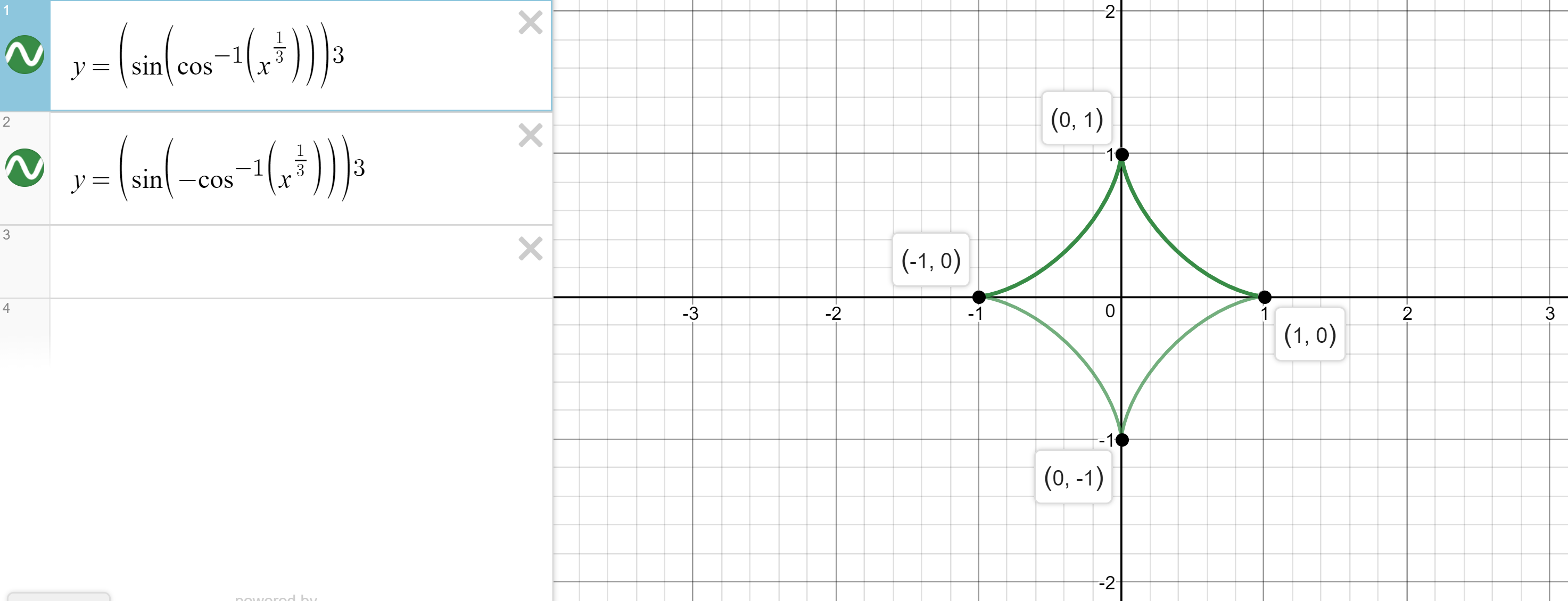 Desmos
Desmos
What we want to do in the cartesian system is if
NOTE that this is only applicable when
Now, we integrate:
skipping integration steps here for time's sake



