What is the area of the triangle ABC?

Points #M# and #N# are sides' midpoints.
#BN# ⊥ #CM#;
#BN = 8#cm and #CM = 12#cm

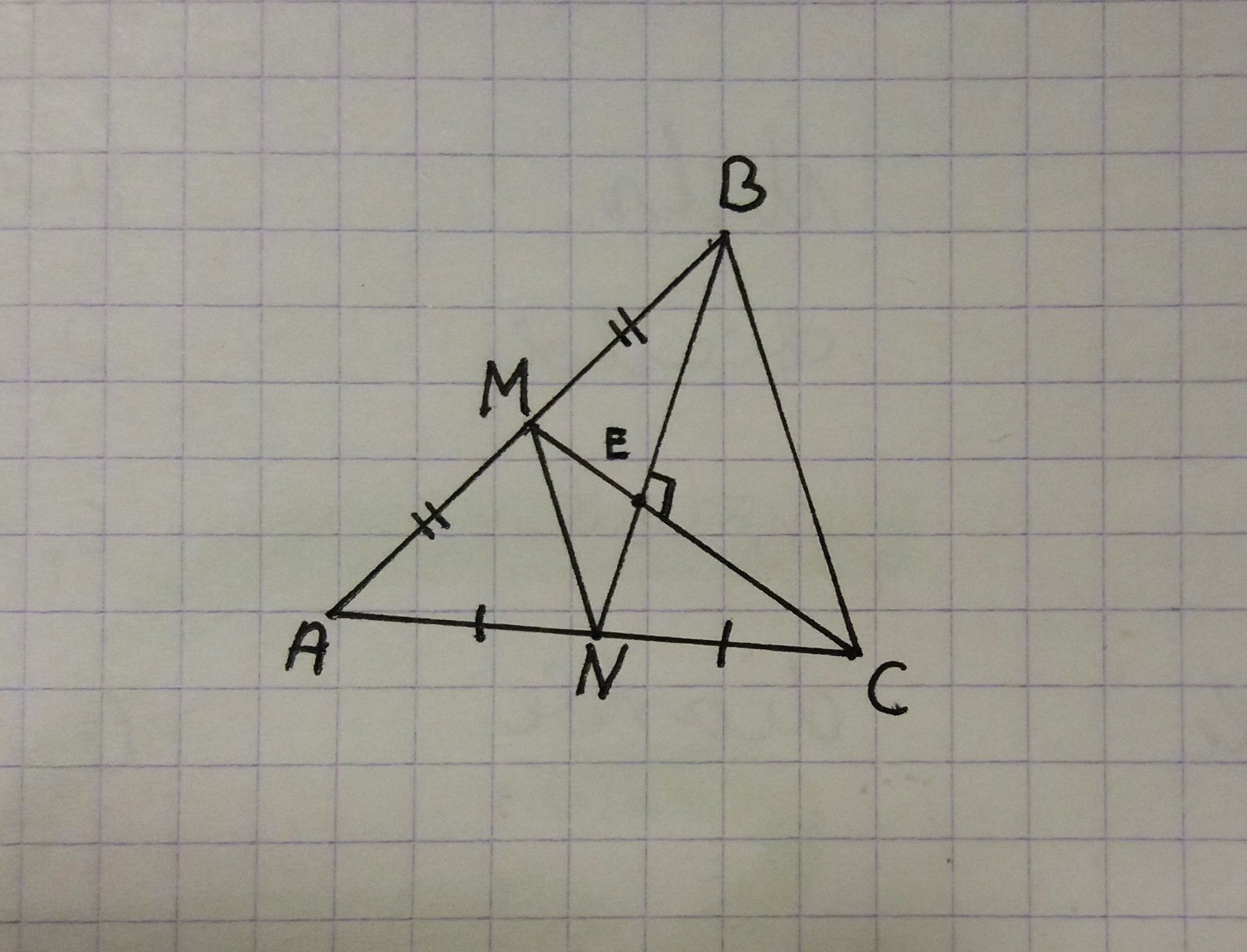
enter image source here

I know, that the answer is #64 cm^2#, but I need a solution step by step.

1 Answer
CW
Oct 31, 2017

area of #DeltaABC=64 " cm"^2#

Explanation:

Let #|ABC|# denote area of #DeltaABC#
As #AM:AN=AB:AC, => MN and BC# are parallel,
#=> DeltaABC and DeltaAMN# are similar,
as #AM:AB=1:2#,
#|AMN| : |ABC|=1:2^2=1:4#
#=> |AMN|:|MNCB|=1:3#
given #BN# is perpendicular to #CM#,
#=> |MNCB|=(BN*CM)/2=(8*12)/2=48#
#=> |AMN|=(|MNCB|)/3=48/3=16#
#=> |ABC|=|AMN|+|MNCB|=16+48=64 " cm"^2#

Related questions
Impact of this question
1302 views around the world
You can reuse this answer
Creative Commons License