Question

What is the centroid of a triangle with corners at `(5, 2 )`, `(2, 5 )`, and `(5,3 )`?

Answer 1

`" "`
`color(blue)("Centroid: (4, 3.bar(3))`

Explanation:

`" "`
`color(red)("Vertices: (5,2), (2,5), and (5,3)`

`color(green)("Step 1"`

Construct a Triangle `ABC: color(blue)(A(5,2), B(2,5), and C(5,3)`

`color(green)("Step 2"`

In a triangle, a Median is a line joining a vertex with the mid-point of the opposite side.

A triangle has three sides, so every triangle has exactly three medians, each running from one vertex to the side exactly opposite.

Let the Mid-Points of the line-segments `color(blue)(bar(AB), bar(BC), bar(AC` be `color(red)(M_1, M_2, and M_3`.

Connect:

`color(blue)("Vertices " A, B and C color(red)(" to the Mid-Points " M_1, M_2, and M_3` respectively.

`color(green)("Step 3"`

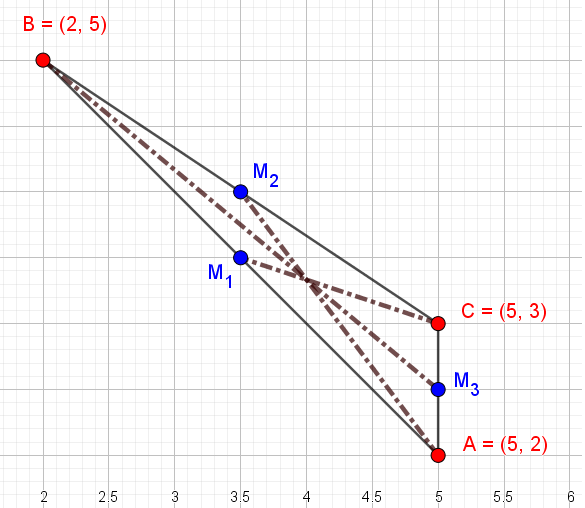
The medians of a triangle are concurrent and the point of concurrence is the Centroid.

`color(green)("Step 4"`

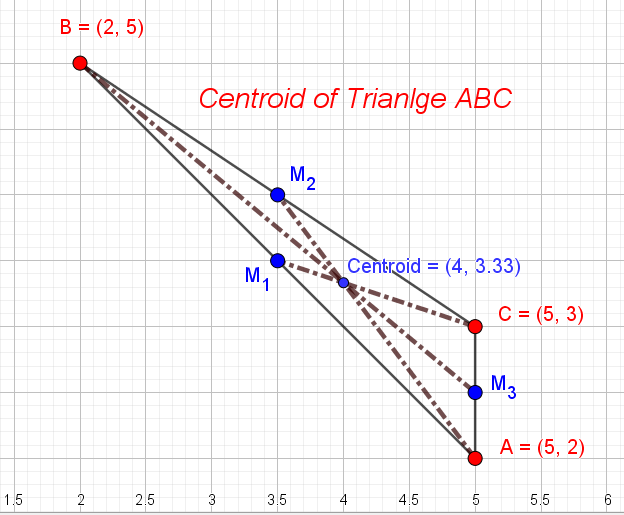
To find the Centroid of a triangle, you can use the formula:

`color(blue)([(x_1+x_2+x_3)/3], [(y_1+y_2+y_3)/3]`

We have,

`(x_1, y_1)=(5,2), (x_2, y_2)=(2,5), and (x_3,y_3)=(5,3)`

`rArr [(5+2+5)/3],[(2+5+3)/3]`

`rArr (12/3, 10/3)`

`rArr (4, 3.bar(3))`

`color(green)("Step 5"`

Some interesting properties of Centroid:

The Centroid divides the length of each median in 2:1 ratio.

Also, observe that the three medians of a triangle divide the triangle into six triangles that are all equal in area.

Hope it helps.