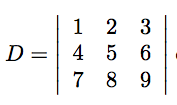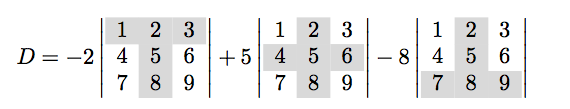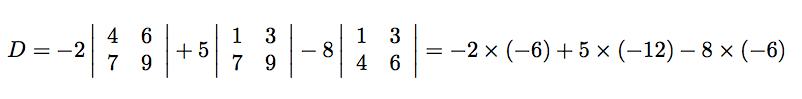Hello !
Let #A = (a_{i,j})# be a matrix of size #n\times n#.
Choose a column : the column number #j_0# (I'll write : "the #j_0#-th column").
The cofactor expansion formula (or Laplace's formula) for the #j_0#-th column is
#\det(A) = \sum_{i=1}^n a_{i,j_0} (-1)^{i+j_0}\Delta_{i,j_0}#
where #\Delta_{i,j_0}# is the determinant of the matrix #A# without its #i#-th line and its #j_0#-th column ; so, #\Delta_{i,j_0}# is a determinant of size #(n-1)\times (n-1)#.
Note that the number #(-1)^{i+j_0}\Delta_{i,j_0}# is called cofactor of place #(i,j_0)#.
Maybe it looks like complicated, but it's easy to understand with an example. We want calculate #D# :
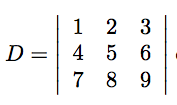
If we develop on the 2nd column, you get
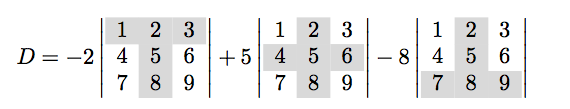
so : 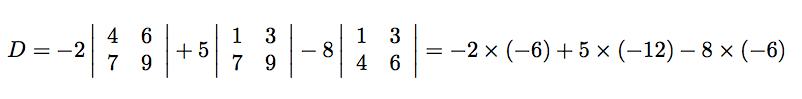
Finally, #D=0#.
To be efficient, you have to choose a line which has a lot of zeros : the sum will be very simple to calculate !
Remark. Because #\det(A) = \det(A^\text{T})#, you can also choose a line rather a column. So, the formula becomes
#\det(A) = \sum_{j=1}^n a_{i_0,j} (-1)^{i_0+j}\Delta_{i_0,j}#
where #i_0# is the number of the selected line.