Question

What is the component of a force of 200 N at a direction 60° to the force?

Answer 1

The parallel component is `vecF_(x)=100N`, the perpendicular component is `vecF_y=100sqrt(3)N`.

Explanation:

The force has both a parallel and perpendicular component. We can see that more clearly if we look at the force vector, `vecF`.

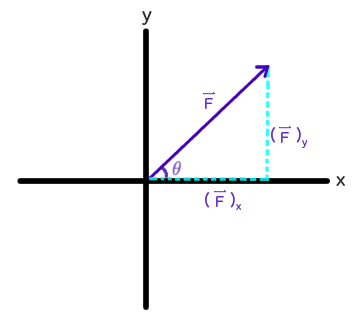
The force has been broken down into its parallel (`x`, horizontal) and perpendicular (`y`, vertical) components.

We see that this forms a right triangle, and in this case, with an angle of `60^o`, we have a special `30^o-60^o-90^o` right triangle. This means we can calculate exact values for each component without using a calculator. I will not include a lesson on the unit circle in this answer, but would be happy to explain in a message if help is needed.

By basic trigonometry, we know that the sine of an angle of a right triangle is found by the ratio of the length of the opposite side to the length of the hypotenuse. In this case, the opposite side is `vecF_y` and the hypothenuse is `vecF`.

`sin(theta)=(vecF_y)/(vecF)`

We can rearrange to solve for `vecF_y`:

`vecF_y=vecFsin(theta)`

Similarly, we know that the cosine of the angle is found by the ratio of the length of the adjacent side to the length of the hypotenuse.

`cos(theta)=(vecF_x)/vecF`

We can rearrange to solve for `vecF_x`:

`vecF_x=vecFcos(theta)`

Using our known values, `vecF=200N` and `theta=60^o`, we can calculate the components:

`vecF_y=200*sin(60^o)=100sqrt(3)N` (`~~173N`)

`vecF_x=200*cos(60^o)=100N`

You can also check your answer using the Pythagorean theorem:

`(vecF_x)^2+(vecF_y)^2=(vecF)^2`

`sqrt((vecF_x)^2+(vecF_y)^2)=vecF`

`sqrt((100)^2+(100sqrt(3))^2)=200`

`sqrt(40000)=200`

`200=200`