Question

What is the converse of the Alternate Interior Angles Theorem?

Answer 1

Converse of the Alternate Interior Angles Theorem:
If alternate interior angles formed by two lines with an intersecting traversal are congruent
then these two lines are parallel.

Explanation:

Let's recall the Alternate Interior Angles Theorem.
If two lines are parallel
then alternate interior angles formed by these two lines with an intersecting traversal are congruent.

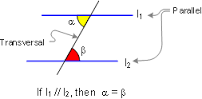
The above figure illustrates this theorem that can be symbolically expressed as

`IF (l_1 || l_2) THEN (alpha=beta)`
or
`(l_1 || l_2) => (alpha=beta)`

Here the premise of a theorem is
two lines are parallel.

The conclusion is
alternate interior angles formed by these two lines with an intersecting traversal are congruent.

Converse theorem is the one obtained by taking a conclusion as a premise of a theorem and a premise - as conclusion.
So, it would look like this:
If alternate interior angles formed by two lines with an intersecting traversal are congruent
then these two lines are parallel.

Using the same figure above, this converse theorem can be symbolically expressed as

`IF (alpha=beta) THEN (l_1 || l_2)`
or
`(alpha=beta) => (l_1 || l_2)`