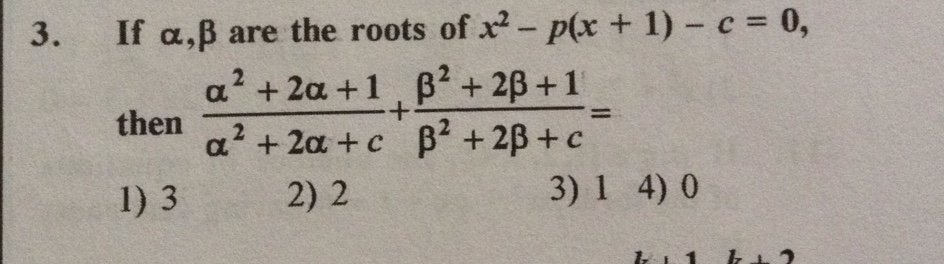Given:
#alpha# and #beta# roots of #x^2-p(x+1)-c = 0#
Use the distributive property and mark as equation [1]:
#x^2-px-p-c = 0" [1]"#
Because #alpha# and #beta# roots of a quadratic equation, the following is also true:
#(x - alpha)(x - beta) = 0#
Perform the multiplication:
#x^2 -betax - alphax+ alphabeta#
Combine like terms and mark as equation [2]:
#x^2 -(alpha+ beta)x+ alphabeta" [2]"#
Matching the coefficient of the middle term in equation [1] with the same term in equation [2]:
#p = alpha+beta" [3]"#
Matching the constant terms of equation [1] with the constant term of equation [2]:
#-p-c = alphabeta#
Solve for c:
#c = -alphabeta-p" [4]"#
Substitute equation [3] into equation [4]:
#c = -alphabeta-(alpha+beta)#
Distribute the minus:
#c = -alphabeta-alpha-beta" [4.1]"#
I found an equation for #c# in terms of #alpha# and #beta#, because we are asked for the value of:
#(alpha^2+2alpha+1)/(alpha^2+2alpha+c) + (beta^2+2beta+1)/(beta^2+2beta+c)#
Substitute for c:
#(alpha^2+2alpha+1)/(alpha^2+2alpha-alphabeta-alpha-beta) + (beta^2+2beta+1)/(beta^2+2beta-alphabeta-alpha-beta)#
Combine like terms in the denominators:
#(alpha^2+2alpha+1)/(alpha^2+alpha-alphabeta-beta) + (beta^2+2beta+1)/(beta^2+beta-alphabeta-alpha)#
Factor the denominators:
#(alpha^2+2alpha+1)/((alpha+1)(alpha-beta)) + (beta^2+2beta+1)/((beta+1)(beta-alpha))#
Please observe that the numerators are perfect squares:
#(alpha+1)^2/((alpha+1)(alpha-beta)) + (beta+1)^2/((beta+1)(beta-alpha))#
#(alpha+1)/(alpha+1)# becomes 1 and #(beta+1)/(beta+1)# becomes 1:
#(alpha+1)/(alpha-beta) + (beta+1)/(beta-alpha)#
We can have a common denominator, if we multiply the second fraction by #-1/-1#:
#(alpha+1)/(alpha-beta) - (beta+1)/(alpha-beta)#
Combine over the common denominator:
#((alpha+1) - (beta+1))/(alpha-beta)#
The 1s in numerator sum to zero:
#(alpha - beta)/(alpha-beta)#
This fraction is 1, therefore, the answer is option 3) 1