To evaluate inverse trigonometric functions, a valuable technique is implicit differentiation:
#d/dxf(y) = d/dyf(y)dy/dx#
In this case, we also will use the chain rule:
#d/dxf(g(x)) = f'(g(x))g'(x)#
as well as the following derivatives:
#d/dxcsc(x) = -csc(x)cot(x)#
#d/dxx^n = nx^(n-1)#
Now, let #y = "arccsc"(sqrt(x+1))#
#=> csc(y) = csc("arccsc"(sqrt(x+1))) = sqrt(x+1)#
#=> d/dxcsc(y) = d/dxsqrt(x+1)#
Through implicit differentiation:
#d/dxcsc(y) = d/dycsc(y)dy/dx = -csc(y)cot(y)dy/dx#
And through the chain rule
#d/dx(x+1)^(1/2) = 1/2(x+1)^(-1/2)(d/dx(x+1)) = 1/(2sqrt(x+1))#
So
#-csc(y)cot(y)dy/dx = 1/(2sqrt(x+1))#
#=> dy/dx = -1/(2sqrt(x+1)*csc(y)cot(y))#
But we want our final answer entirely in terms of #x#. To fix this, we remember that #csc(y) = sqrt(x+1)# and draw a corresponding right triangle:
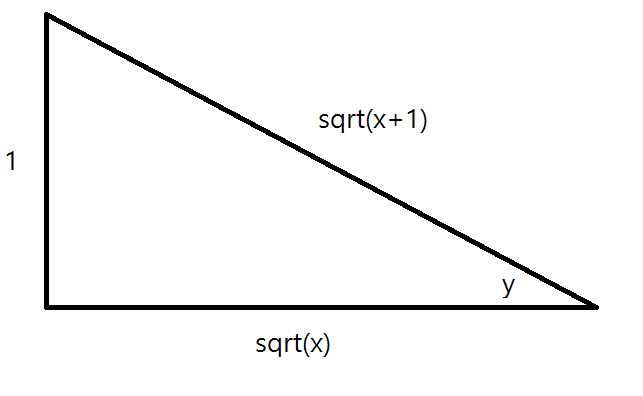
From this we can see that #cot(y) = sqrt(x)#
Thus we have
#-1/(2sqrt(x+1)*csc(y)cot(y)) = -1/(2sqrt(x+1)*sqrt(x+1)*sqrt(x))#
From this, we can get our final answer
#d/dx "arccsc"(sqrt(x+1)) = -1/(2(x+1)sqrt(x))#



