Use the Chain Rule and some algebra to simplify:
#d/dx(arcsin(sqrt{1-x^2}))#
#=1/sqrt{1-(sqrt{1-x^2})^2} * d/dx((1-x^2)^{1/2})#
#=1/sqrt{1-(1-x^2)} * 1/2 (1-x^2)^{-1/2} * (-2x)#
#=-x/(sqrt{x^2} sqrt{1-x^2})#
#=-x/sqrt{x^2-x^4}#
This is true for all #x\in (-1,0) cup (0,1)# (for all #x# strictly between #-1# and #1# except for #x=0#).
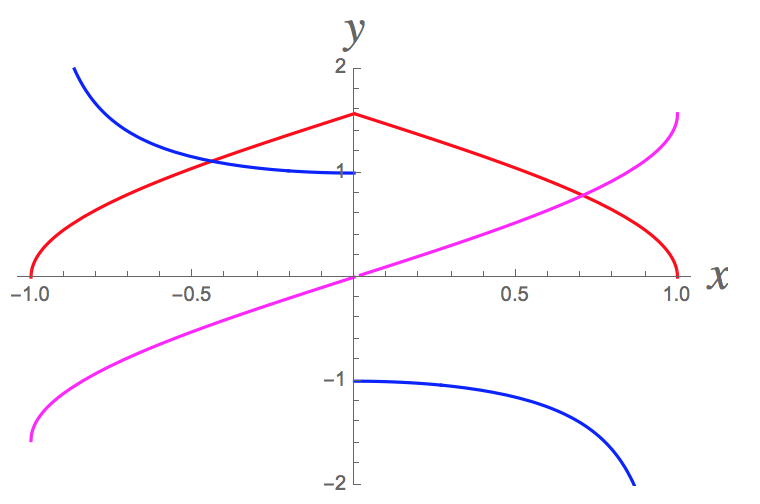
#y=arcsin(sqrt{1-x^2})# is actually pretty interesting since you wouldn't expect ahead of time that it would fail to be differentiable at #x=0#. Here's what the graph of it (red) and its derivative (blue) look like:
The discontinuity in the derivative at #x=0# can also be seen by noting that #sqrt{x^2}=|x|# and therefore #-x/sqrt{x^2}=-x/|x|# equals #-1# when #x>0# and #1# when #x<0#. Therefore, #f'(x)=-1/sqrt{1-x^2}# when #x>0# and #f'(x)=1/sqrt{1-x^2}# when #x<0#.
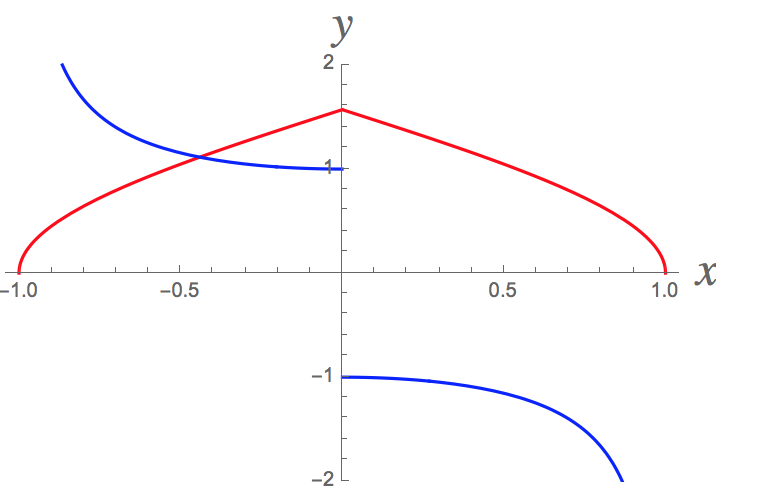
For the original function, #f(x)=arcsin(sqrt{1-x^2})#, evidently it's like taking the graph of #arcsin(x)#, shifting it up by #pi/2# units, and then reflecting the part of it for #x>0# across the horizontal line #y=pi/2#.
In other words, #arcsin(sqrt{1-x^2})=arcsin(x)+pi/2# when #x<0# and #arcsin(sqrt{1-x^2})=pi/2-arcsin(x)# when #x>0#. Weird! Never would have guessed that!
The second equation (for #x>0#) makes sense if you draw a right triangle, label one angle #arcsin(sqrt{1-x^2})#, label the adjacent side #sqrt{1-x^2}# and the hypotenuse #1#, then solve for the other side with the Pythagorean Theorem to get #x#. In that situation, #arcsin(x)# would be the complementary angle to the original one, illustrating why #arcsin(sqrt{1-x^2})=pi/2-arcsin(x)# when #x>0#.
Here's a graph of the original #f(x)# and #f'(x)#, along with #arcsin(x)# to illustrate all this: