What is the difference between a jump and a removable discontinuity?
1 Answer
Nov 14, 2015
Their limit definitions and appearance on a graph.
Explanation:
This is a jump discontinuity. 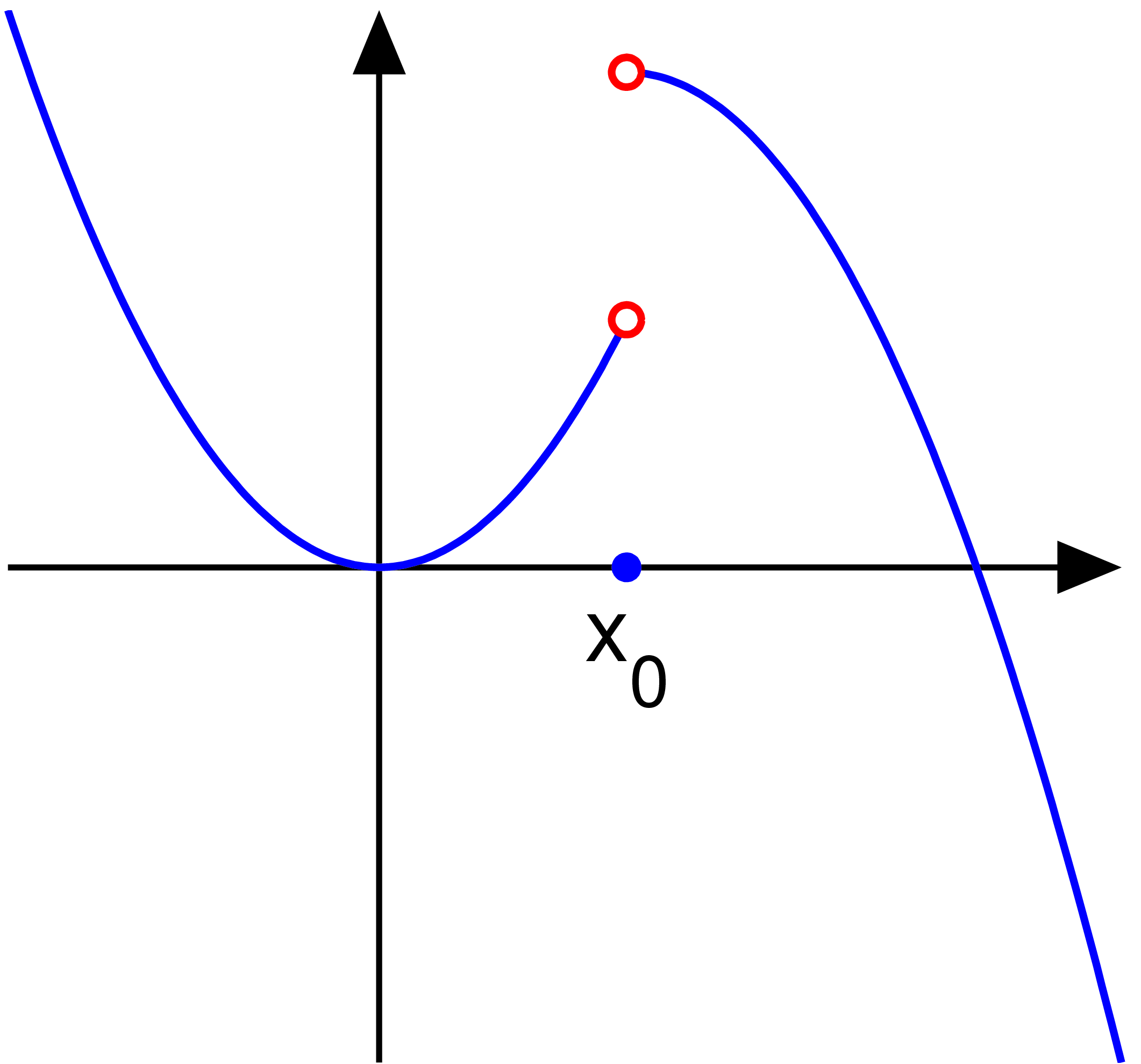
In a jump discontinuity,
This is a removable discontinuity (sometimes called a hole).
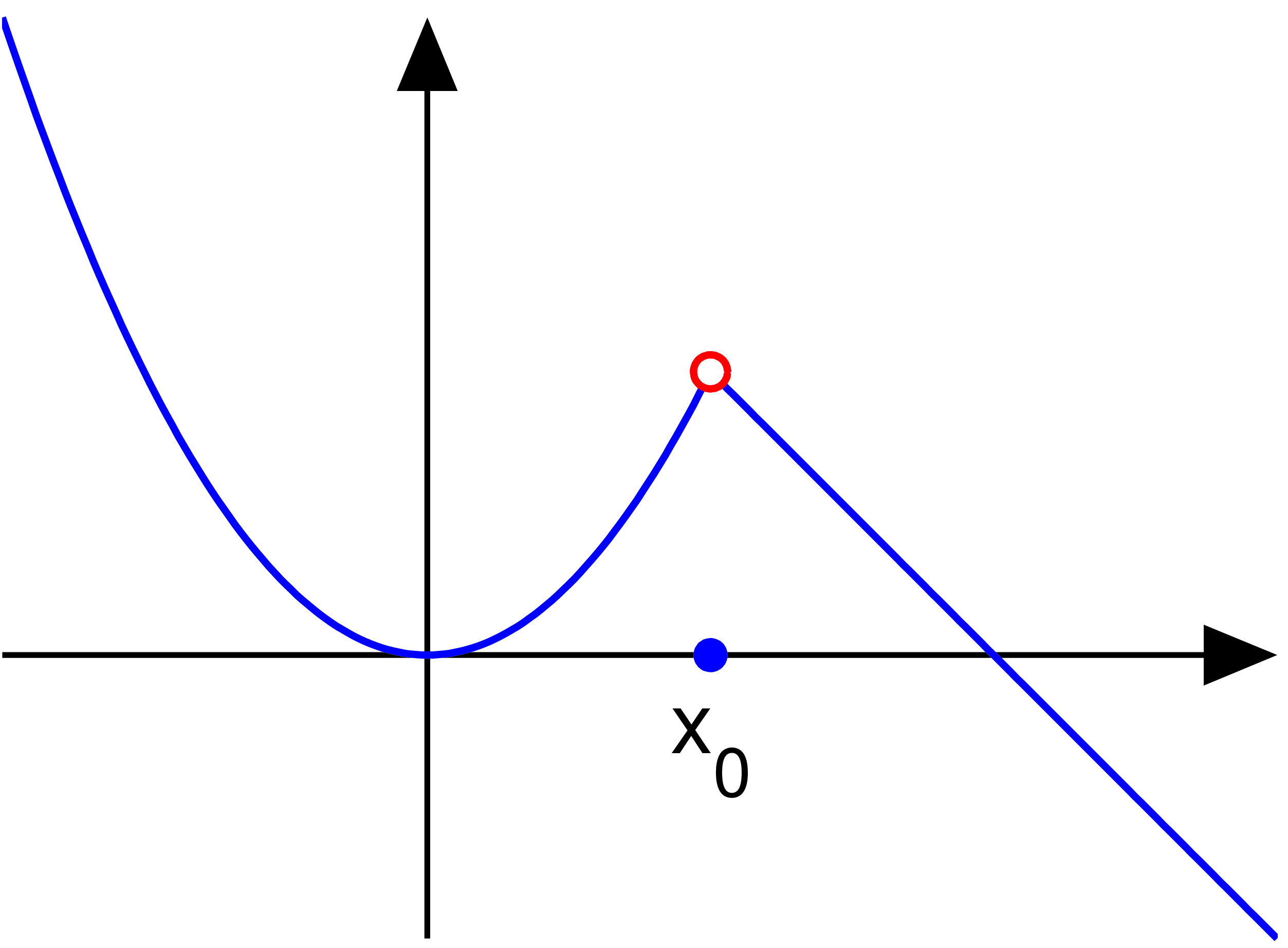
Here, the function appears to come to a point, but the actual function value is elsewhere or does not exist.This can be written as

