What is the difference between a Tangent line and a secant line on a curve?
1 Answer
The tangent line to a curve at a given point is a straight line that just "touches" the curve at that point.
So if the function is f(x) and if the tangent "touches" its curve at x=c, then the tangent will pass through the point (c,f(c)). The slope of this tangent line is f'(c) ( the derivative of the function f(x) at x=c).
A secant line is one which intersects a curve at two points.
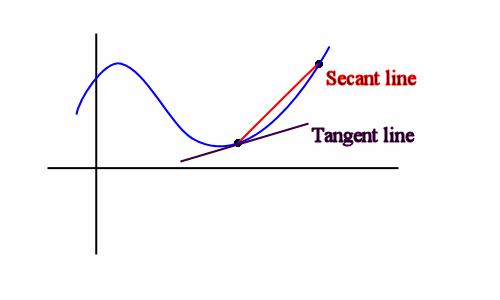
Click this link for a detailed explanation on how calculus uses the properties of these two lines to define the derivative of a function at a point.


