What is the difference between alternate and corresponding angles?
1 Answer
See the picture and explanation below.
Explanation:
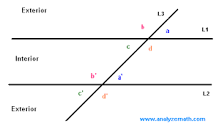
When two parallel lines are intersected by the third (transversal), they form eight angles: one of the parallel lines forms four angles
Two acute angles
So are other pairs (acute and obtuse) similarly positioned:
One of corresponding angles is always interior (in between parallel lines) and another - exterior (outside of the area in between parallel lines).
Two acute angles
So are other pairs (acute and obtuse) similarly positioned:
The alternate angles are either both interior or both exterior.
The classical theorem of geometry states that corresponding angles are congruent. The same for alternate interior and alternate exterior angles.

