Renal Plasma Flow
In practice, it is difficult to measure #RPF# directly.
Instead, it is estimated from the effective renal plasma flow (#ERPF#), which is the amount of plasma cleared of p-aminohippuric acid (#PAH#) per unit time.
The formula for #RPF# comes from the Fick relation, which is really a mass balance calculation.
#"Flow in = flow out"#
#"renal artery input = renal vein output + ureter output"#
#RPF × P_a = RPF × P_v + U × V#
where
#P_a and P_v "= arterial and venous plasma concentrations of PAH"#
#U "= urine concentration of PAH"#
#V "= urine flow rate"#
Rearranging gives:
#color(blue)(bar(ul(|color(white)(a/a)RPF = (UV)/(P_a-P_v)color(white)(a/a)|)))" "#
Almost all the #PAH# is cleared through the ureter.
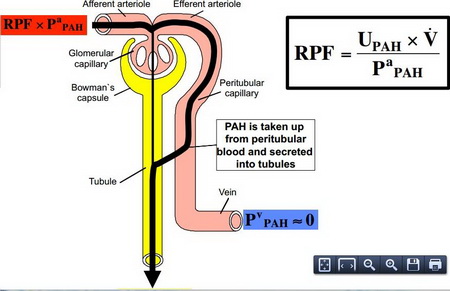
(From slideplayer.com)
Setting #P_v = 0# gives
#color(blue)(bar(ul(|color(white)(a/a)ERPF = (UV)/P_acolor(white)(a/a)|)))" "#
Renal Blood Flow
#RBF# is the measure of blood (plasma + RBCs) that passes through the kidneys.
#"blood = plasma + hematocrit"#
Let #Hct = "fraction of blood that is RBCs"#
Then #"fraction that is plasma" = 1 - Hct# and
#RBF(1-Hct) =ERPF#
#color(blue)(bar(ul(|color(white)(a/a) RBF = (ERPF)/(1-Hct)color(white)(a/a)|)))" "#
Sample Problem
Calculate #RBF# for a patient with the following: #U "= 650 mg/mL"#; #V "= 1 mL/min"#; #P_a "= 1.2 mg/mL"#; #Hct "= 0.45"#.
Solution
#ERPF = (UV)/P_a = (650 color(red)(cancel(color(black)("mg/mL"))) "× 1 mL/min")/(1.2 color(red)(cancel(color(black)("mg/mL")))) = "542 mL/min"#
#RBF = (ERPF)/(1-Hct) = "542 mL/min"/(1 - 0.45) = "542 mL/min"/0.55 = "985 mL/min"#


