What is the difference between t = 0 and t = 1 seconds?
2 Answers
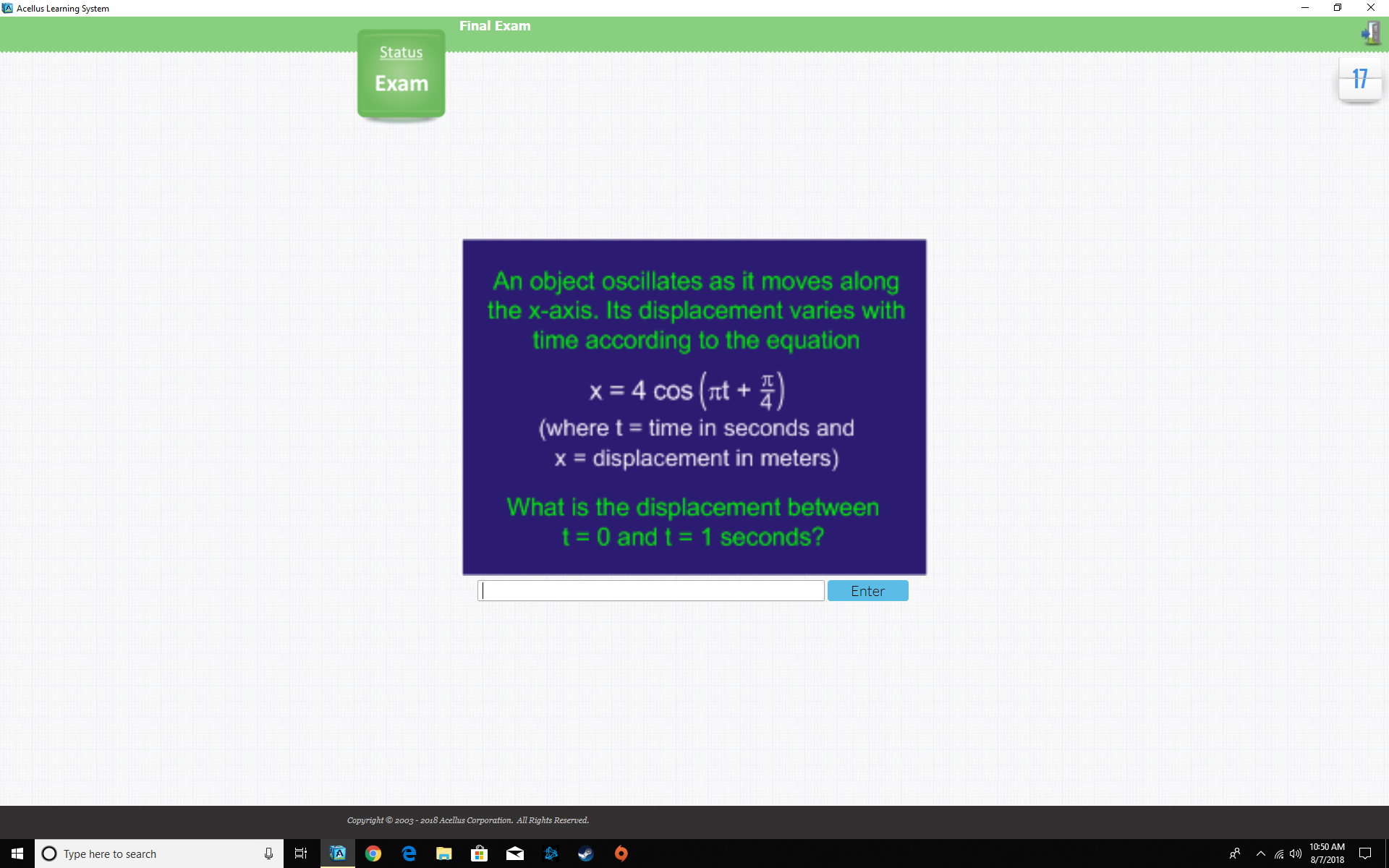
Given displacement vector
#x=4cos(pit+pi/4)#
Value of
#x(0)=4cos(pixx0+pi/4)#
#=>x(0)=4cos(pi/4)#
Value of
#x(1)=4cos(pixx1+pi/4)#
#=>x(1)=4cos((5pi)/4)#
Displacement between
#Deltax=x(1)-x(0)#
#=>Deltax=4cos((5pi)/4)-4cos((5pi)/4)#
#=>Deltax=4[cos((5pi)/4)-cos((pi)/4)]#
Making use of the unit circle reproduced below to rewrite in vector form. The first value in the round brackets represents
#=>Deltax=4[-sqrt2/2hatj-sqrt2/2hatj]#
#=>Deltax=-4sqrt2hatj#
This is 1-D motion, along the number line:
-
#x(t) = 4 cos (pi t + pi / 4)# -
#{(x(0) = 4 cos (pi /4) = 4/sqrt2),(x(1) = 4 cos ((5pi) /4) = - 4/sqrt2 ):}#

