Question

What is the direction and magnitude of the magnetic field the particle is traveling? What is the direction and magnitude of the magnetic field the second particle is traveling?

A 9.9 x 10^-5C charged particle is traveling east, with speed 4.0 x 10^5 m/s. The particle feels a force of 0.24 N going south, due to a large bar magnet. A second particle of charge 2.7 x 10^-4C is traveling upward, with speed 2.0 x 105 m/s. The particle feels a force of 0.26 N going south, due to a large bar magnet.

Answer 1

`(a)`

`"B"=0.006" ""N.s"` or `"Tesla"` in a direction coming out of the screen.

Explanation:

The force `F` on a particle of charge `q` moving with a velocity `v` through a magnetic field of strength `B` is given by:

`F=Bqv`

`:. B=F/(qv)`

`B=0.24/(9.9xx10^(-5)xx4xx10^5)=0.006" ""N.s"`

These 3 vectors of magnetic field `B`, velocity `v` and force on the particle `F` are mutually perpendicular:

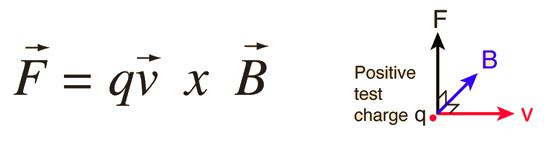
Imagine rotating the above diagram by `180^@` in a direction perpendicular to the plane of the screen.

You can see that a +ve charge moving from left to right across the screen (east) will feel a force vertically downwards (south) if the direction of the field `B` is out of the screen.

`(b)`

The 2nd part of the question does not make sense to me. The force must be perpendicular to the motion and not in an opposite direction, as described in the question.