Question

What is the discontinuity of the function `f(x) = (x^2-3x-28)/(x+4)` ?

Answer 1

If a rational expression (basically a fraction with a polynomial in the numerator and another polynomial in the denominator) has a discontinuity, it will be where the denominator equals zero.

So for `f(x)=(x^2-3x-28)/(x+4)`, the only possible discontinuity would be when

`x+4=0`

or

`x=-4`

Now there are two types of discontinuity possible here.

If `x+4` is also a factor of the numerator, you will have what's called a removable discontinuity. That will show up as a hole in the graph.

If `x+4` is not a factor of the numerator, then you will have a vertical asymptote at `x=-4`.

Let's see:

`f(x)=(x^2-3x-28)/(x+4)`

`f(x)=((x+4)(x-7))/(x+4)`

`f(x)=x-7`, as long as x doesn't equal `-4`.

The discontinuity is removable. The graph would look like the line `f(x)=x-7` except at `x=-4`, there is a hole.

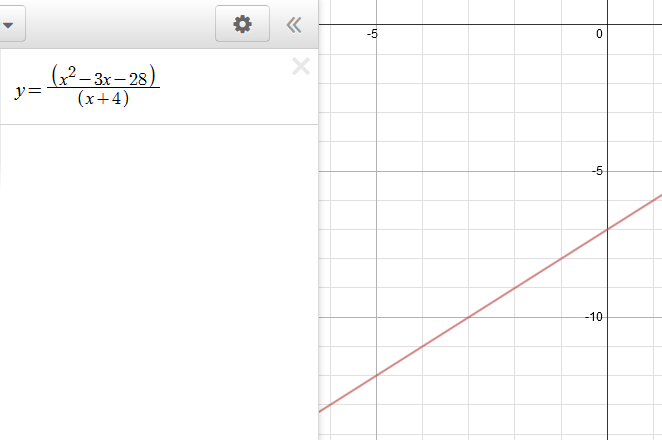
Note that most graphers will not properly show a hole (as in this case); this is known as a graphing error.