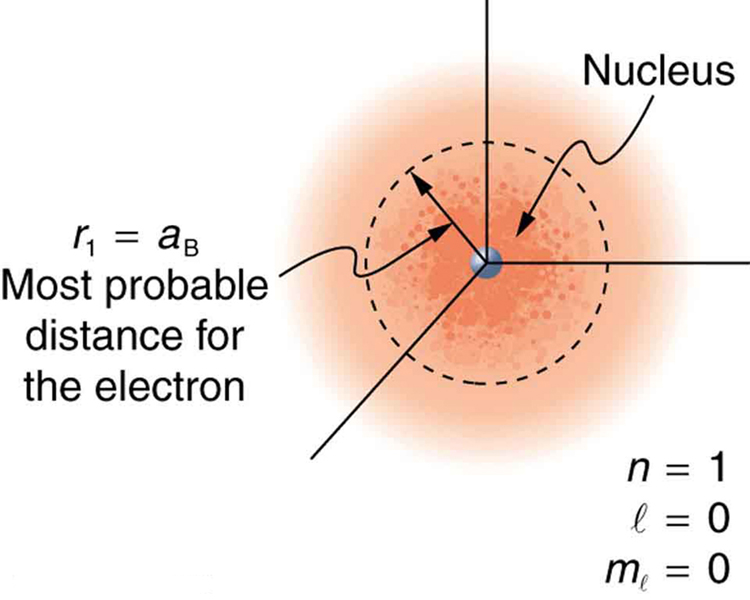
What is the distance an electron is from a proton?
1 Answer
It varies from atom to atom. Often it is hard to predict, and it is a much better idea to focus on hydrogen-like atoms when learning about it. We have to use a most probable distance.
In hydrogen atom, it is relatively straightforward; the
I am unsure as to how these electron-nucleus separations compare to other hydrogen-like atoms (
In atoms that contain more than one electron, there exists electron-electron correlation that complicates the location of each electron in space.
- For helium, we have electron-electron correlation, which is instantaneous short-range repulsions (dynamical correlation), as well as some set of degenerate electron configurations (nondynamical correlation, though not significant).
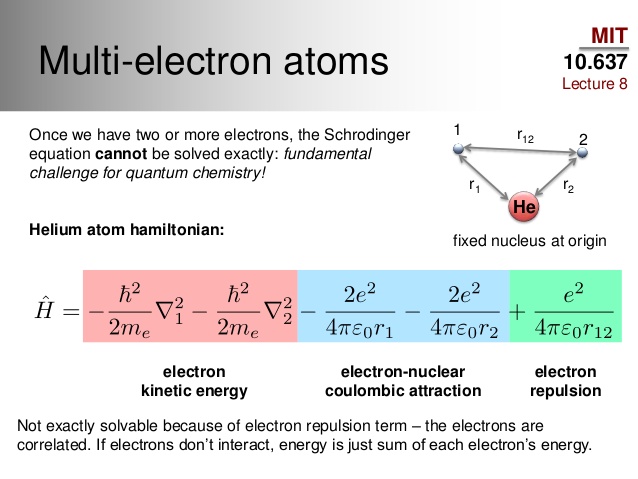
We can approximate the probability density by assuming a one-electron approximation, wherein we take an average electron density and ignore electron-electron repulsions.

Then, we make special corrections to account for such repulsions, such as the variational theorem or nth-order perturbation theory.
Therefore, we only get an approximate ground-state energy for helium, from which we can acquire an inexact, most-probable electron-nucleus distance.
- For atoms with more than two electrons (
#"Li"# ,#"Be"# , etc), it gets harder and harder to make good approximations, and we computational chemists are trying to determine better and better ways to make special approximations and "corrections" to get more and more exact ground-state energies.