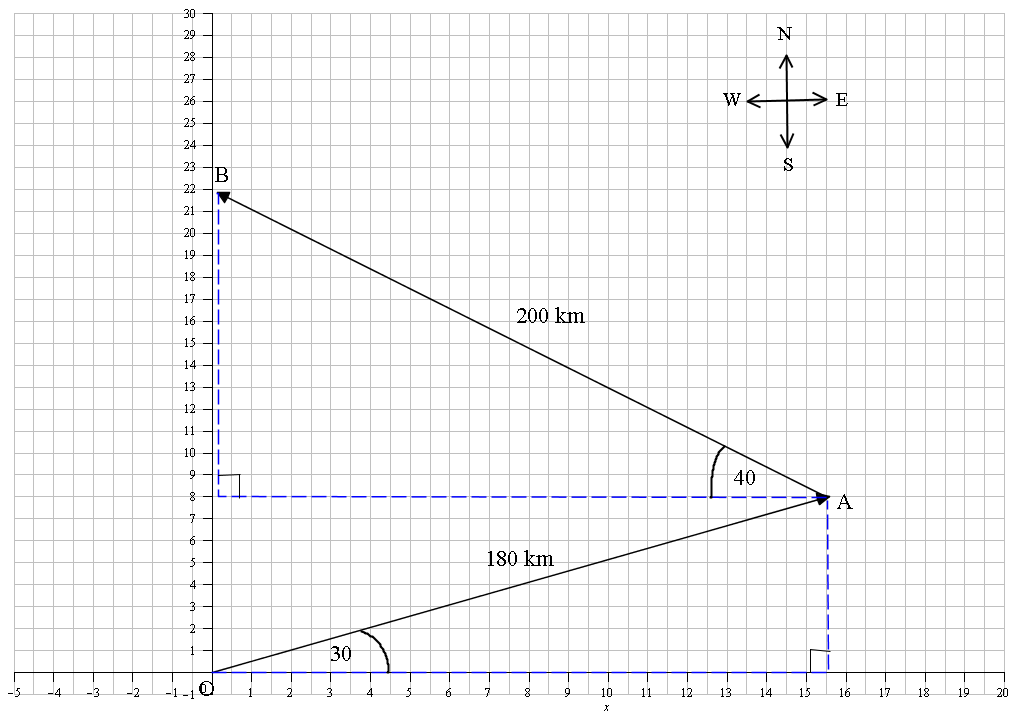
From the diagram we can see that the bearing #30^@# north of east makes an angle of #30^@# with the x axis, and the bearing #40^@# north of west makes an angle of #40^@# with the x axis. If we represent these as in the diagram we form two right angled triangles, with the hypotenuse being the magnitude of the displacement. Our task is to find the vector components that represent these displacements. Using the origin as our base camp O.
Let # \ \ \ \vec(OA)# be the displacement 180 km north of east.
and # \ \ \ \vec(AB)# be the displacement 200 km north of west.
Looking at the lower triangle representing #vec(OA)# and using unit vectors #bbi# and #bbj# to represent the x and y directions respectively. By trigonometry we have:
#vec(OA)=180cos(30)bbi+180sin(30)bbj#
For #vec(AB)# and its related triangle we need to think about the direction of the #bbi# component. This is opposite to the #bbi# component of #vec(OA)# and so its sign will be negative. Also because we generally measure angles in an anti clockwise direction from the positive x axis our angle of #40^@# would then be #180-40= 140^@#. This will give the correct sign when using the cosine function. So:
#vec(AB)=200cos(140)bbi+200sin(140)bbj#
We need to find the distance and direction from B to O.
By vector addition we have:
#vec(BO)=vec(OA)+vec(AB)#
#vec(BO)=[180cos(30)bbi+180sin(30)bbj]+[200cos(140)bbi+200sin(140)bbj]#
Adding like components:
#vec(BO)=[180cos(30)+200cos(140)]bbi+[180sin(30)+200sin(140)]bbj#
Simplifying where possible.
#vec(BO)=[90sqrt(3)+200cos(140)]bbi+[90+200sin(140)]bbj#
This has exact values for the components.
For the direction we can first find the angle this vector makes with the positive x axis and then convert it to a direction in term of the compass point.
Angle with x axis is:
#tan(theta)=(bbj)/(bbi)=(90+200sin(140))/(90sqrt(3)+200cos(140))#
#theta=arctan((90+200sin(140))/(90sqrt(3)+200cos(140)))=89.298593100583^@#
The #bbj# component in #vec(BO)# is negative so we are heading in a southerly direction. With some thought we can see that this is:
#0.7^@# east of south.
The distance is given by the magnitude of #vec(BO)#
#||vec(BO)||=sqrt((90sqrt(3)+200cos(140))^2+(90+200sin(140))^2)#
#=218.57km# 2 d.p.




