Question

What is the domain of `f(x) = sqrt[cos(sinx)]`?

Answer 1

all real numbers (`RR`)

Explanation:

treat this as a composition of functions:

outer function: `sqrt(x)`
middle function: `cos(x)`
inner function: `sin(x)`

work from outer function to inner:

for a value of x to produce a real output, the value in the `sqrt()` must be `>=0`. that means `cos(sinx)>=0`

for `cos()` to give a value `>=0`, the input of `cos()` must be in the interval: `[-pi/2+2pik,pi/2+2pik]`, where k is any integer. some of these intervals include: `[(-5pi)/2,(-3pi)/2], [-pi/2,pi/2], [(3pi)/2,(5pi)/2]`

this means `sinx` must be in one of those intervals. `sinx` will never be `>1` or `<-1` so you can ignore all previous intervals except `[-pi/2,pi/2]`, which contains all the possible outputs of `sin(x)`

now, the only restriction is that `sinx` must be in the interval `[-pi/2,pi/2]`, which happens to be true for any real number `x`.

so the domain is all real numbers (`RR`)

Answer 2

We have our radical function given to us:

`color(blue)(f(x) = sqrt(cos(sin(x)))`

The domain is

`color(green)(-oo < x < +oo)`

Using the Interval Notations

`(-oo, +oo)`

Explanation:

We have our radical function given to us:

`color(blue)(f(x) = sqrt(cos(sin(x)))`

Please refer to the graph of this radical function below:

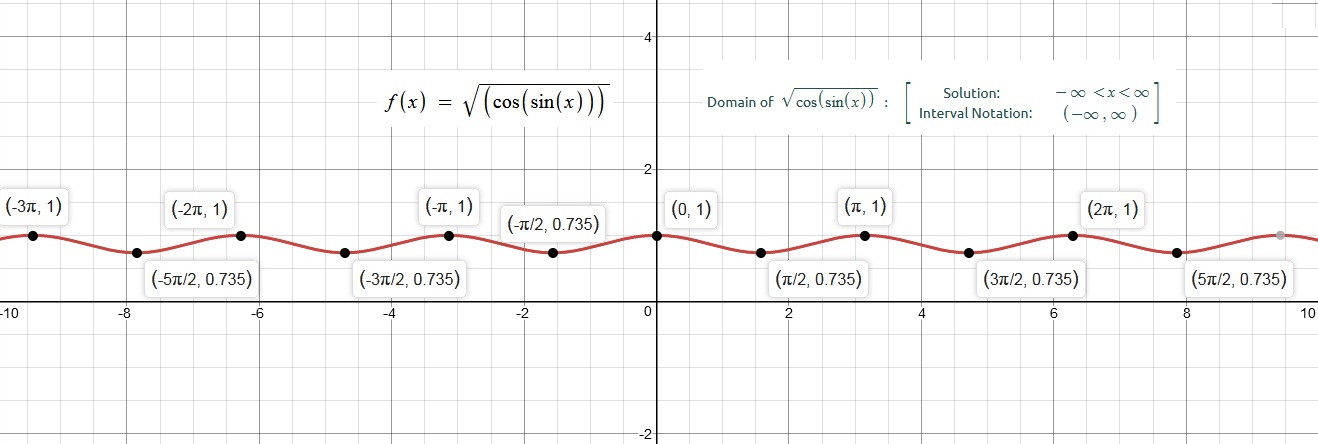
When we analyze the graph above, we observe that the given radical function does not have any undefined points and we also observe that three are no domain constraints.

Therefore,

The domain is

`color(green)(-oo < x < +oo)`

Using the Interval Notations we can write our domain as

`(-oo, +oo)`