What is the domain of the function?
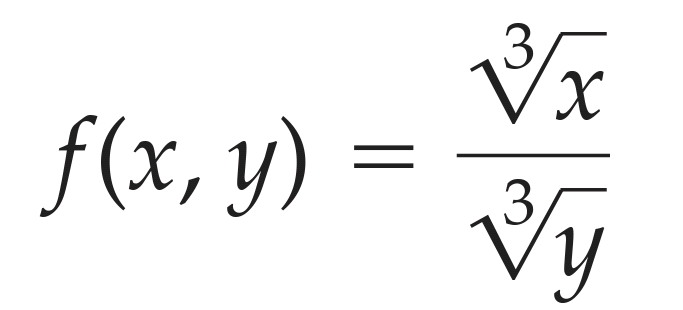
1 Answer
Apr 8, 2018
Explanation:
Recall that the domain is the set of valid inputs to the function. In this case, it is the set of all pairs
Also recall that, while you cannot take the square root of a negative number, you can take the cube root of a negative number. For example,
Additionally,
Thus, our domain is
Note: This can be more concisely written as

