What is the domain of #y = 2sinx+ 1#?
1 Answer
Sep 7, 2014
The domain of the sine function is all Real numbers, or
That means that this function will continue to repeat its values infinitely to the left and right along the x-axis. (see graph)
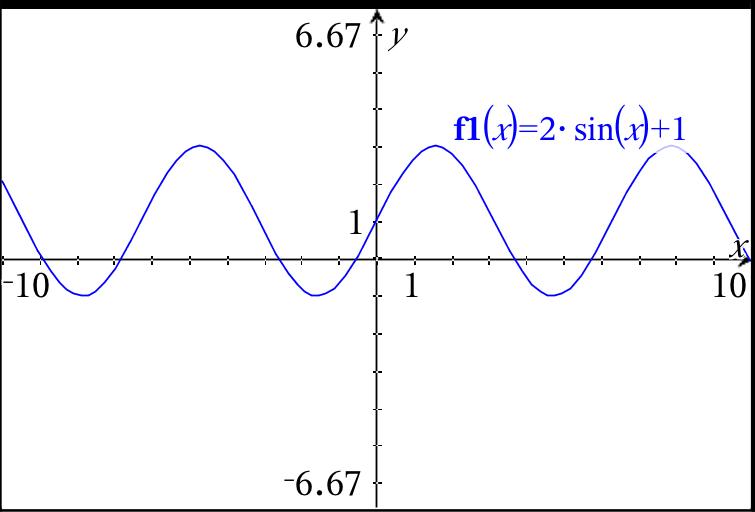
It might be beneficial to talk about the range of this function. The normal sine function graph oscillates between -1 and 1. Written in interval notation, this would be
This function, y = 2sin(x) + 1 has undergone a vertical stretch (multiplied by 2) as well as a vertical translation of up 1. Look at the graph to see the new minimum and maximum of -1 and 3. Thus, the range is [-1,3].

