What is the empirical formula for a compound containing 38.8 g carbon, 16.2 g hydrogen and 45.1 g nitrogen?
2 Answers
Explanation:
To find the empirical formula change the mass to moles Then find a ratio between the moles.
For Carbon
For Hydrogen
For Nitrogen
The ratio for Carbon and Nitrogen is
The ratio of Hydrogen to both Carbon and Nitrogen is 5:1
So the ratio is 1 C to 1 N to 5 H.
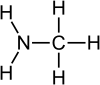
Nitrogen usually forms three bonds one to Carbon and 2 to Hydrogen atoms. Carbon usually forms four bonds one to Nitrogen and 3 to Hydrogen atoms.
The empirical formula is
This may be methylamine,
Explanation:
The empirical formula of a compound represents the simplest whole number ratio of elements in the compound.
We must first determine the moles of each element in the compound by dividing the given mass by the molar mass.
Since the masses of all of the elements equal
To determine the subscripts of the empirical formula, we find the lowest whole number ratio for each element by dividing the moles of each element by the least number of moles, in this case
The empirical formula is
Note: If the mol ratios are not all whole numbers, you will need to multiply each mole ratio by the same factor that will make all mol ratios whole numbers.
This may be methylamine,