Question

What is the end behavior of the function `f(x) = 5^x`?

Answer 1

The graph of an exponential function with a base > 1 should indicate "growth". That means it is increasing on the entire domain. See graph:

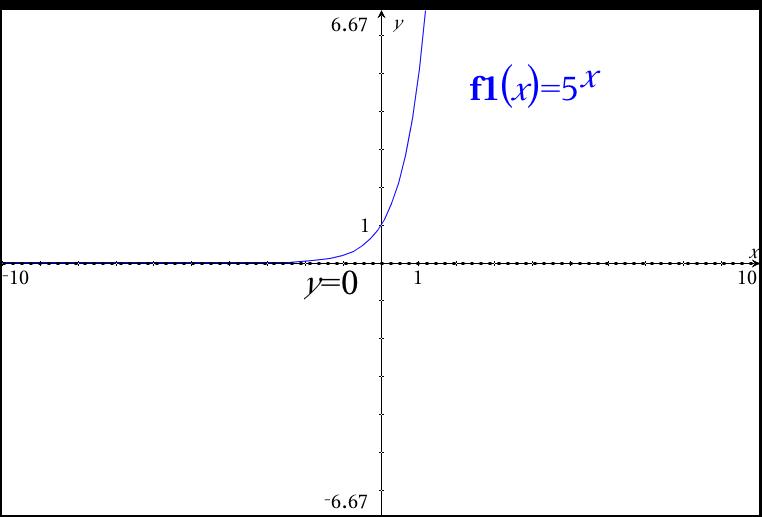
For an increasing function like this, the end behavior at the right "end" is going to infinity. Written like: as `xrarr\infty,yrarr\infty` .
That means that large powers of 5 will continue to grow larger and head toward infinity. For example, `5^3=125`.

The left end of the graph appears to be resting on the x-axis, doesn't it? If you calculate a few negative powers of 5, you will see that they get very small (but positive), very quickly. For example: `5^-3=1/125` which is a pretty small number! It is said that these output values will approach 0 from above, and will never equal exactly 0! Written like: as `xrarr\-\infty,yrarr0^+` . (The raised + sign indicates from the positive side)