Question

What is the equation in standard form of the parabola with a focus at (4,3) and a directrix of y= -3?

Answer 1

`y=1/12x^2-2/3x+4/3`

Explanation:

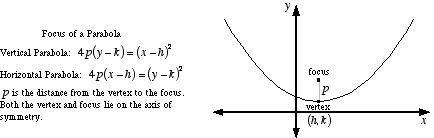mathwords.com

The focus must be the same distance from the vertex as the directrix for this to work. So apply the Midpoint theorem:`M=((x_1+x_2)/2,(y_1+y_2)/2)`
`\therefore((4+4)/2,(3+(-3))/2)` (both have the same x-value for convenience)
which gets you a vertex of `(4,0)`. This means both focus and directrix are 3 vertical units away from the vertex (`p=3`).

Your vertex is the coordinate `(h,k)`, so we input into the vertical parabola format...

`4(3)(y-0)=(x-4)^2`
`12(y-0)=(x-4)^2`

Now we simplify.
`12y-0=(x-4)(x-4)`
`12y=x^2-8x+16`

Standard form is `y=ax^2+bx+c` but we have to isolate the `y` on the left. So divide everything by 12 and you have your answer.

`y=1/12x^2-8/12x+16/12`
`y=1/12x^2-2/3x+4/3`