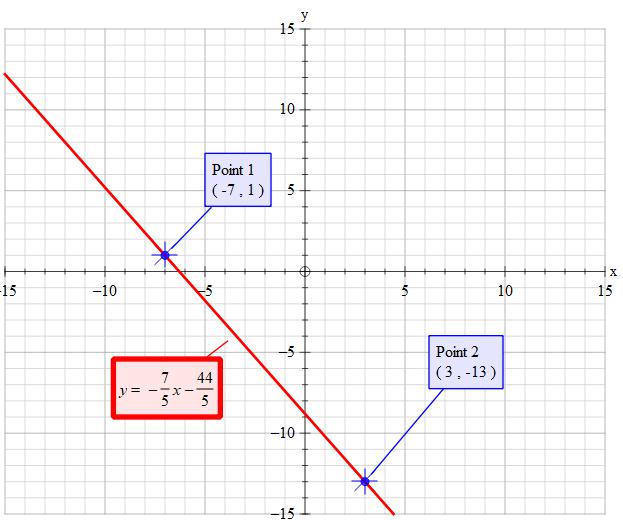
What is the equation of the line between #(3,-13)# and #(-7,1)#?
2 Answers
Explanation:
When you know the coordinates of two points
Plug your values to get
Multiply both sides by
Subtract
Over the top detail given so that you can see where everything comes from.
Explanation:
Using the gradient (slope)
Reading left to right on the x-axis.
Set point 1 as
Set point 2 as
In reading this we 'travel' from
We may choose any of the two:
Add 5 to both sides
Divide both sides by 5
Now using generic