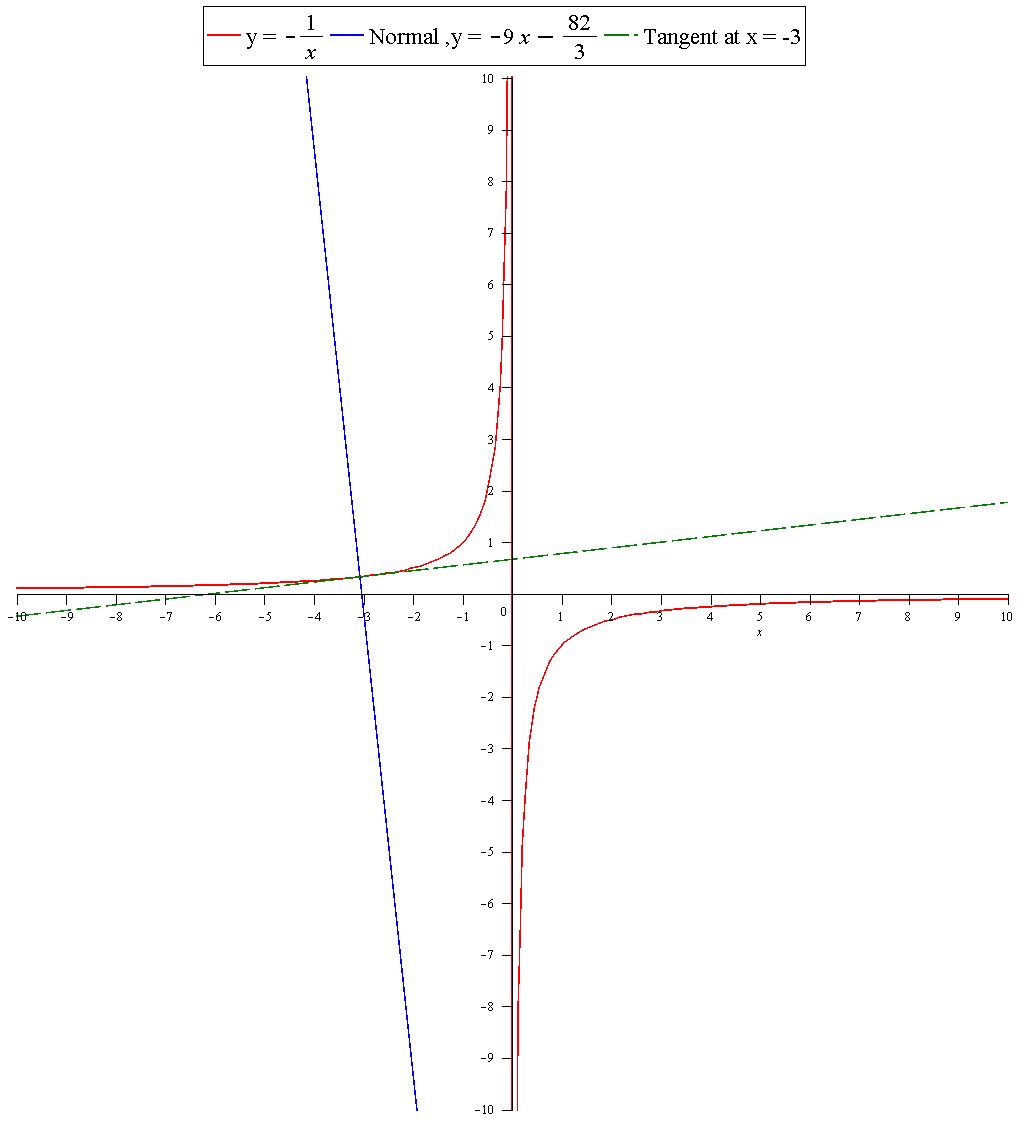
What is the equation of the line normal to #f(x)= -1/x # at #x=-3#?
1 Answer
Mar 12, 2018
Explanation:
The line that is normal to
We first need to find the gradient of the tangent line at
Plugging in
We know that if two lines are perpendicular, then the product of their gradients is
Let gradient of the normal be
The normal passes through the point with x coordinate
Using point slope form of a line:
Graph: