Question

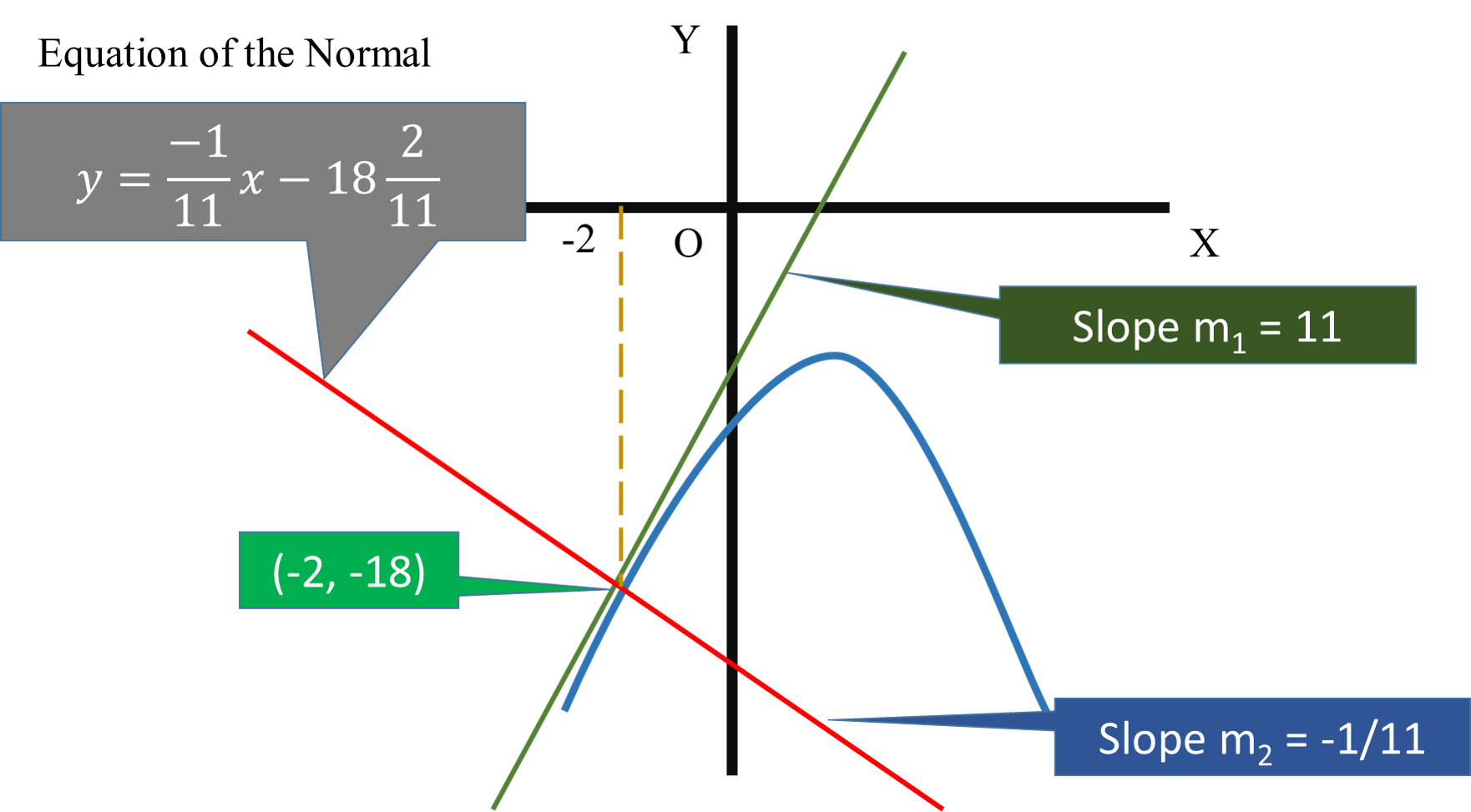
What is the equation of the line normal to `f(x)=-2x^2 +3x - 4` at `x=-2`?

Answer 1

`y=-1/11x-18 2/11`

Explanation:

Given -

`y=-2x^2+3x-4`

The first derivative gives the slope at any given point

`dy/dx=-4x+3`

At `x=-2` its slope is

`dy/dx=-4(-2)+3=8+3=11`

It can be taken as the slope of the Tangent, drawn to that point on the curve.

Y- co-ordinate of the point -

`y=-2(-2)^2+3(-2)-4`
`y=-8-6-4=-18`

The point on the curve, the normal passing through is `(-2, -18)`

If the two lines are perpendicular then -

`m_2 xxm_2=-1`
`11 xx m_2=-1`
`m_2=(-1)/11`

The equation of the normal is -

`mx+c = y`
`-1/11(-2)+c=-18`
`2/11+c=-18`
`c=-18-2/11=18 2/11`

Equation is -

`y=-1/11x-18 2/11`