Question

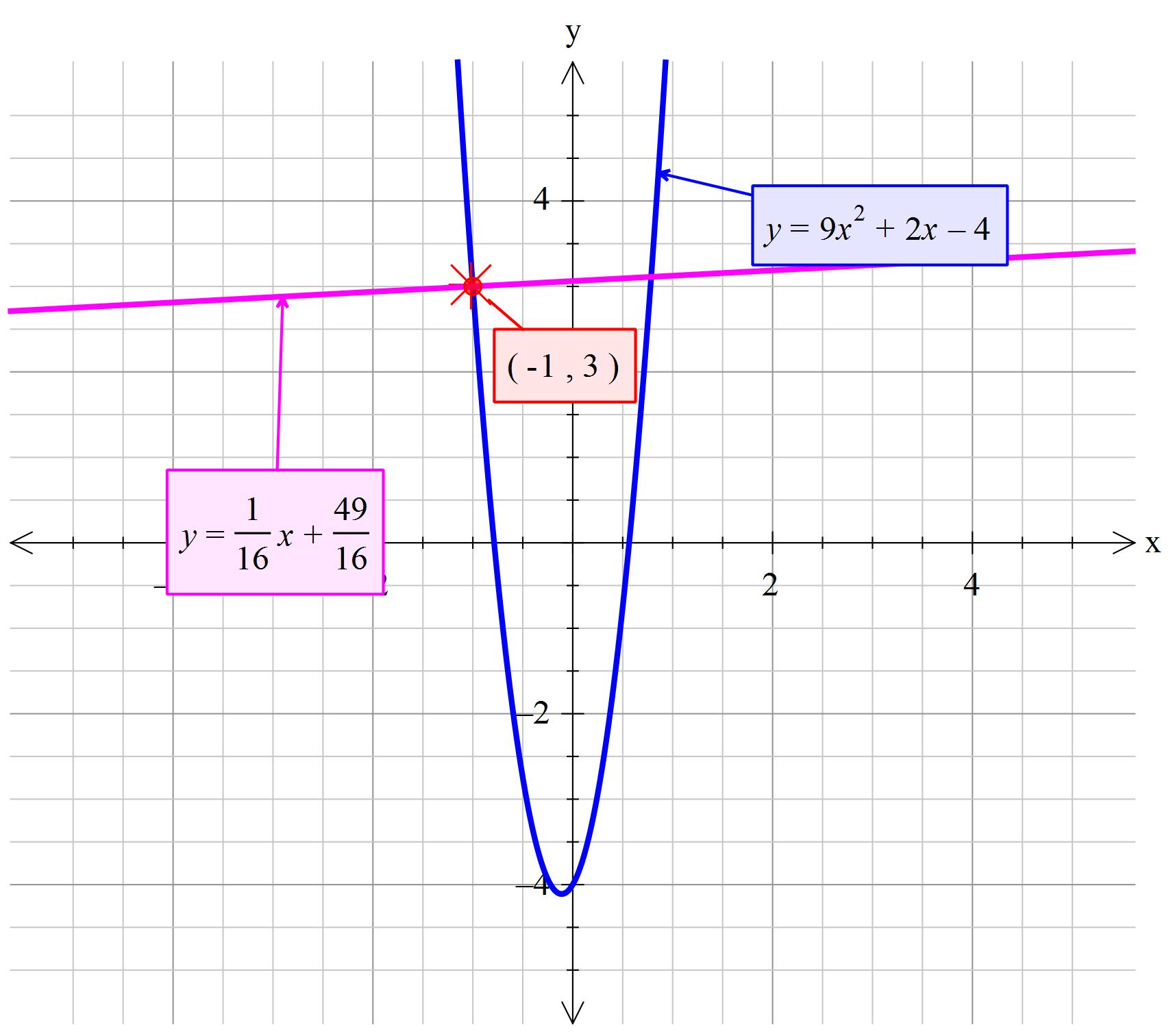
What is the equation of the line normal to `f(x)=9x^2 +2x - 4` at `x=-1`?

Answer 1

`y=+1/16x+49/16`

Explanation:

Let the given point be `P_1->(x_1,y_1)=(-1,y_1)`

Differentiating each term of `f(x)`

`9x^2->2xx9x^(2-1)=18x`

`2x->2`

`-4->0`

So `(dy)/(dx)->f^'(x) = 18x+2`

`=>f^'(-1) = 18(-1)+2 = -16`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Gradient of the line normal to `f(x)" is "(-1)xx1/(-16)` giving:

`" "color(blue)(y=+1/16x+c)` ................................Eqn(1)

This line passes through the point `(x,y)->(-1,y_1)`

Substitute `x_1=-1` into `f(x)->f(-1)" " ->" "y_1= 9(-1)^2+2(-1)-4`

`y_1=9-2-4=+3`

Thus `P_1->(x_1,y_1)=(-1,3)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

So Eqn(1)`->P_1->(x_1,y_1)->y_1=1/16x_1+c" "` becomes

`=>P_1->(x_1,y_1)->3=1/16(-1)+c`

Thus `c=+3 1/16 -> 49/16`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The equation of the line is:

`y=+1/16x+49/16`