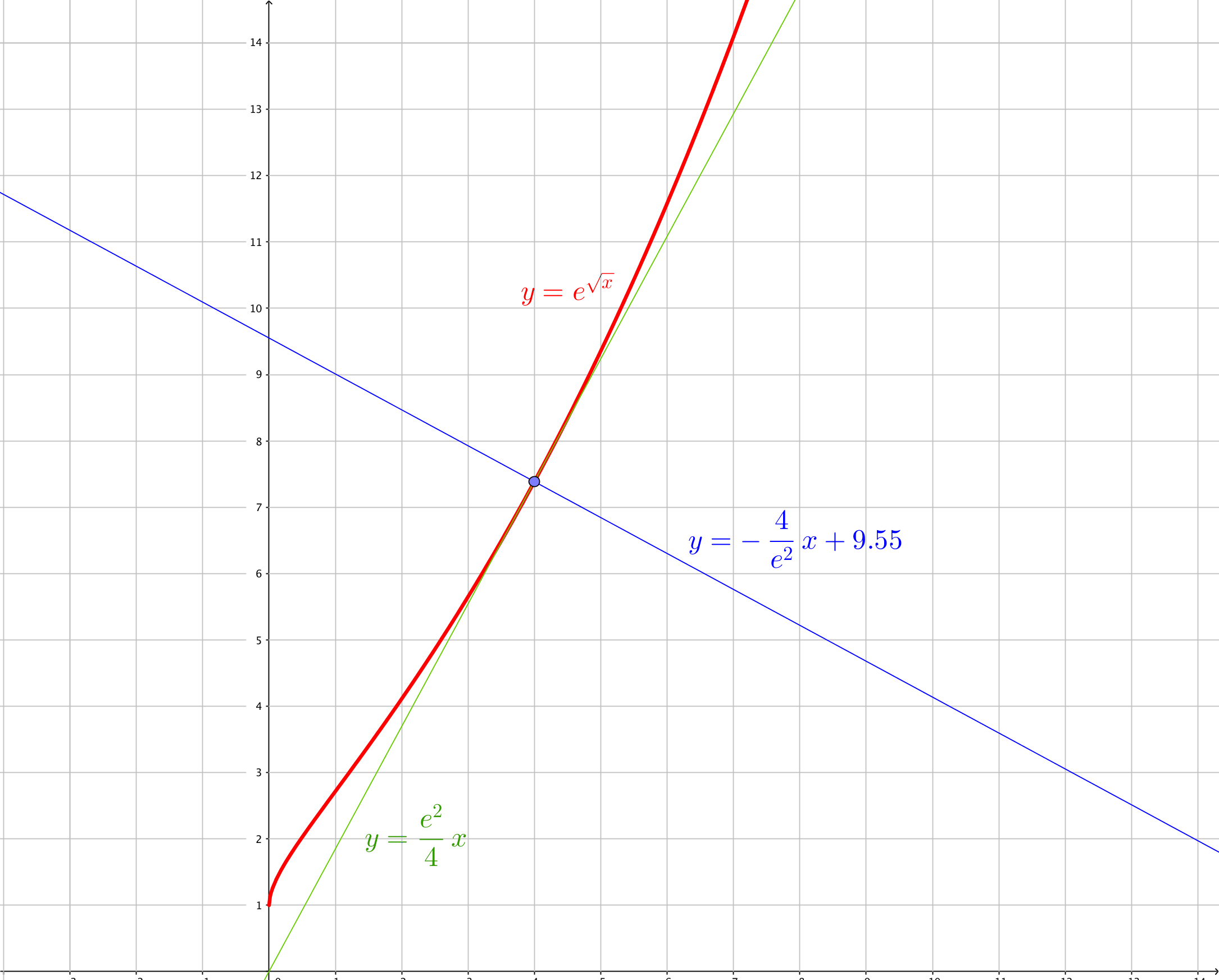
The line passing from #x=4# and tangent to #e^sqrt(x)# has as slope
#d/dxe^sqrt(x)# evaluated when #x=4#. The derivative can be calculated with the chain's rule
#d/dxe^sqrt(x)=e^sqrt(x)*d/dxsqrt(x)=e^sqrt(x)/(2sqrt(x))#.
The slope is
#m=e^sqrt(4)/(2sqrt(4))=e^2/4#.
So the tangent has equation
#y=e^2/4x+q#
The #q# can be found imposing the passage of the line from the point #(4, e^sqrt(4))=(4, e^2)#
#e^2=e^2/4*4+q# then #q=0# and the equation of the tangent is
#y=e^2/4x#
The orthogonal has the negative inverse slope, so the equation is
#y=-4/e^2x+q#
Again, to find #q# we have to impose the passage from #(4, e^2)#
#e^2=-4/e^2*4+q#
#q=e^2+16/e^2=(e^4+16)/e^2\approx9.55# and finally the equation of the orthogonal is
#y=-4/e^2x+9.55# or
#y=-0.54x+9.55#.