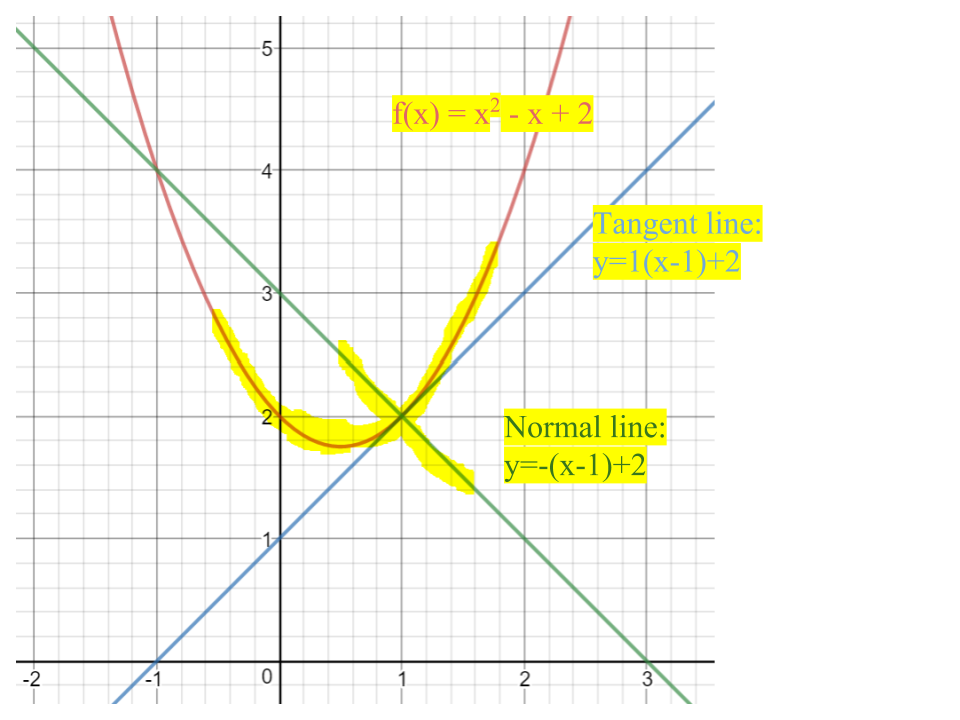
What is the equation of the line normal to f(x)=x^2 -x +2 at x=1?
1 Answer
Aug 1, 2017
Explanation:
First find the equation of the line TANGENT to the function at the point; then find the equation of the line that passes through that point but has a perpendicular slope.
f(1) =1^2-1+2 = 2
We now have the point and the slope of the line tangent to
Simplified tangent line:
Since the slope is
Simplified normal line:
 Desmos, Google Drawings
Desmos, Google Drawings

