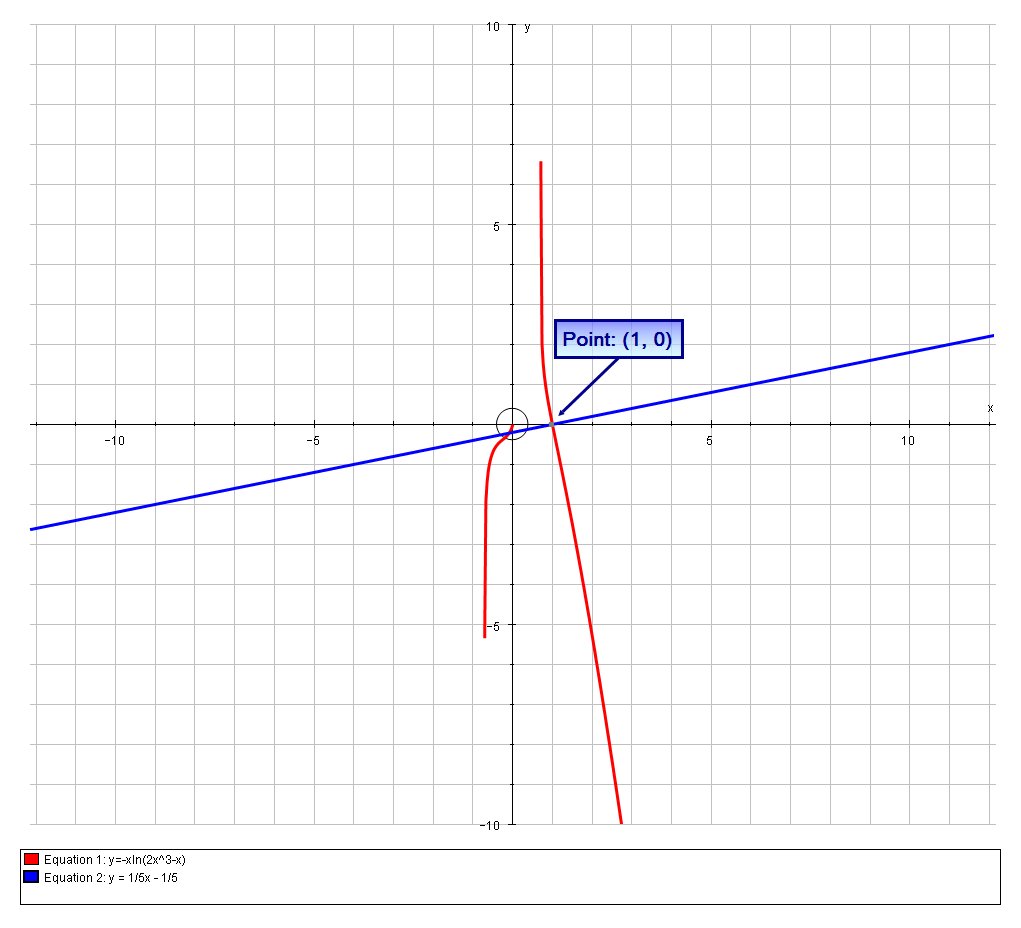
What is the equation of the line normal to # f(x)=-xln(2x^3-x)# at # x=1#?
1 Answer
Explanation:
The gradient of the tangent to a curve at any particular point is give by the derivative of the curve at that point. The normal is perpendicular to the tangent and so the product of their gradients is
so If
# \ \ \ \ \ f'(x) = (-x)(1/(2x^3 - x)*(6x^2 - 1)) + (-1)(ln(2x^3 - x)) #
# :. f'(x) = -(6x^2-1)/(2x^2-1) -ln(2x^3-x) #
When
and
So the tangent passes through
# y-0 = 1/5(x-1) #
# \ \ :. y = 1/5x - 1/5 #
We can confirm this solution is correct graphically: