Question

What is the equation of the line perpendicular to `y=-7/5` that passes through `(-35,5)`?

Answer 1

`x=-35`

Explanation:

Firstly, let's go over what we already know from the question. We know that the `y`-`"intercept"` is `-7/5` and that the slope, or `m`, is `0`.

Our new equation passes through `(-35,5)`, but the slope will not change since 0 is neither positive nor negative. This means that we need to find the `x-"intercept"`. So, our line will be passing through vertically, and have a undefined slope (we don't have to include `m` in our equation).

In our point, `(-35)` represents our `x-"axis"`, and `(5)` represents our `y-"axis"`. Now, all we have to do is pop the `x-"axis"` `(-35)`into our equation, and we're done!

The line that is perpendicular to `y=−7/5` that passes through `(−35,5)` is `x=-35`.

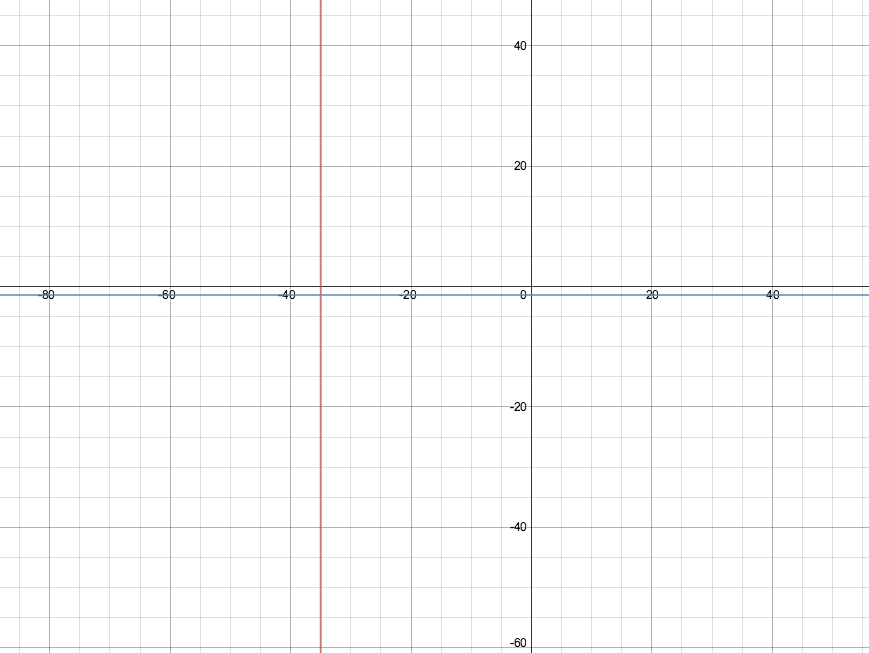
Here's a graph of both lines.

Answer 2

solution is, `x+35=0`

Explanation:

`y=-7/5` represents a straight line parallel to x-axis lying at a distance `-7/5` unit from x-axis.
Any straight line perpendicular to this line should be parallel to y-axis and can be represented by the equation `x=c` ,where c = a constant distance of the line from y-axis.
Since the line whose equation to be determined passes through(-35,5) and is parallel to y-axis, it will be at a distance -35 unit from y-axis. Hence its equation should be `x=-35=>x+35=0`