What is the equation of the line tangent to #f(x)=cosx-sinx# at #x=pi/3#?
1 Answer
Explanation:
First, find the point of tangency. We know the
Substitube in the given value of
Based on what you know about the unit circle and these tutorials, https://www.youtube.com/playlist?list=PLsX0tNIJwRTyXncFO4Z5bxme0mBe2wq0R.
Point of Tangency
Now we need to find the equation of the slope by applying the derivative to
Let substitute in
Now we have to figure out the equation of tangent line by using the slope intercept formula,
Isolate the variable,
Equation of the tangent line,
The 2 images below are to show the point of tangency on the graph.
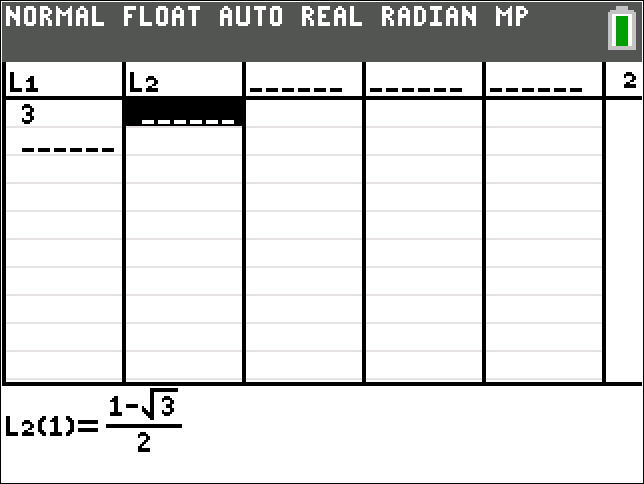
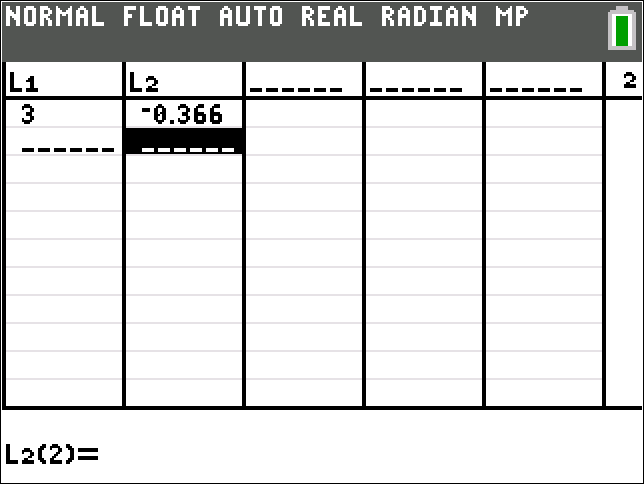
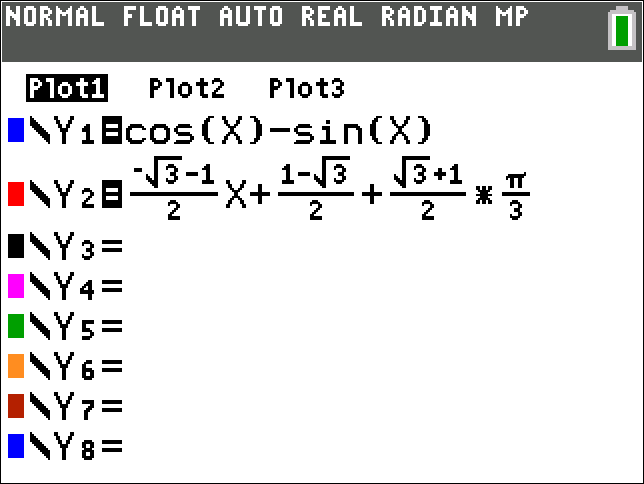
The first equation in blue is
The second equation in red is the tangent line.
The image below is the graph of all of this work.
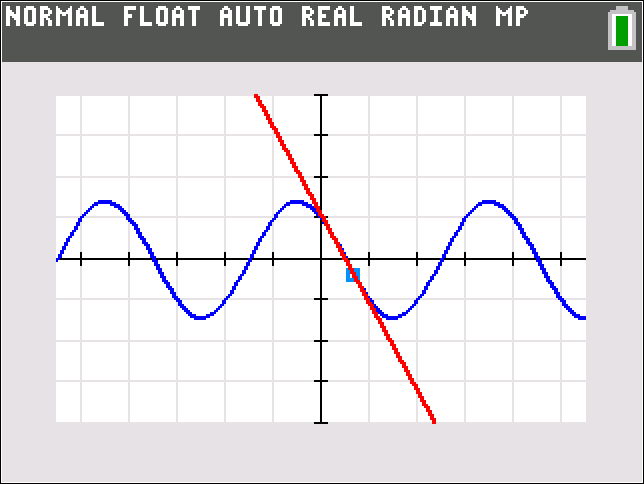
Lastly, I have several tutorials on how to find the equation of the tangent line.
https://www.youtube.com/playlist?list=PLsX0tNIJwRTw2e-oelZuY6TGevXWsTFJ3

