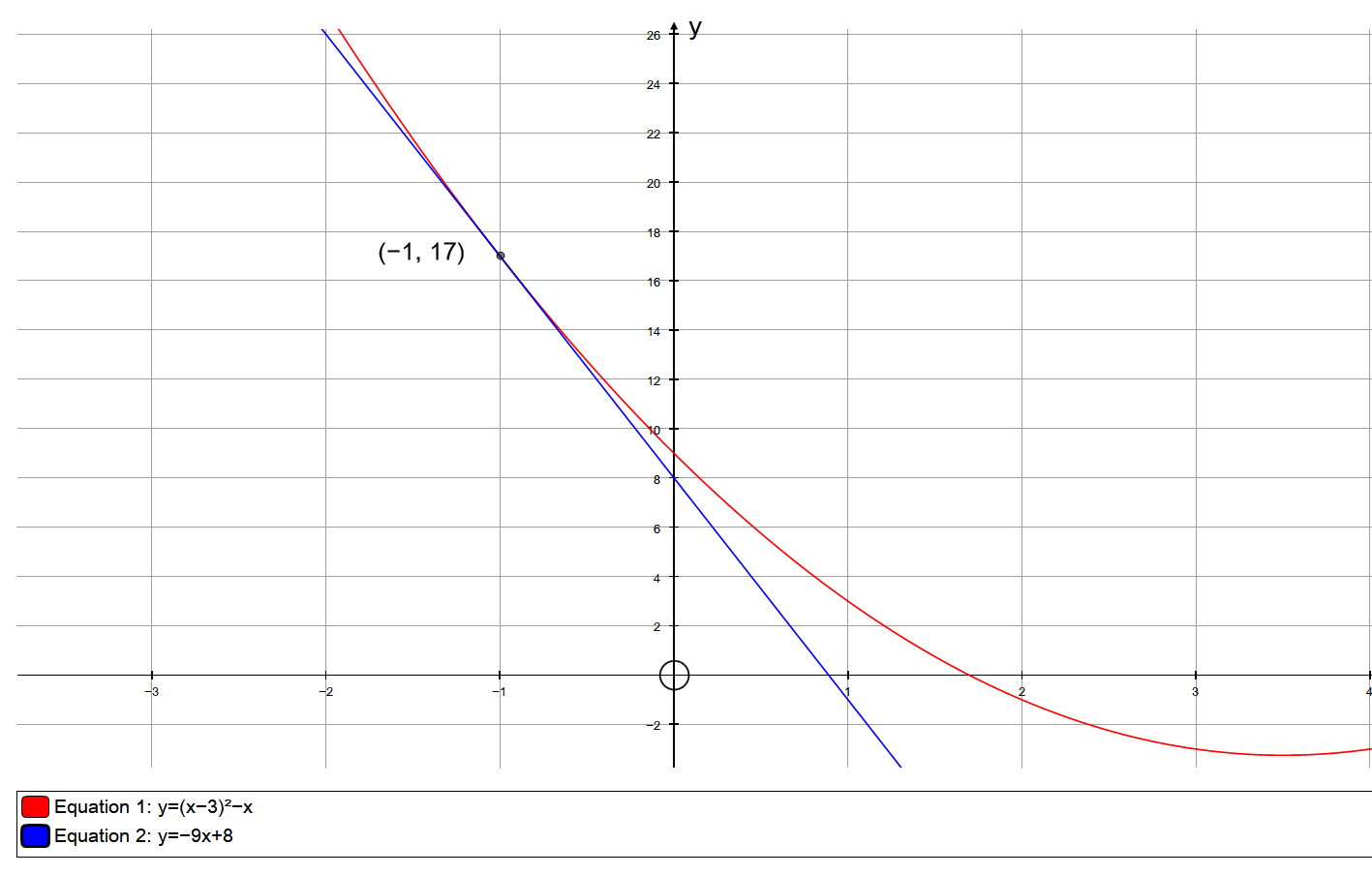
What is the equation of the line tangent to #f(x)=(x-3)^2-x # at #x=-1#?

Question

2779 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-14T16:27:34

#color(blue)(y=-9x+8)#

In order to find the equation of the tangent line, we must first find the gradient of this line at the given point.

To do this we find the derivative of #f(x)#, and then plug in #x=-1#

#f(x)=(x-3)^2-x#

We can expand this and then we only need to use the power rule to differentiate it.

#(x-3)^2-x=x^2-7x+9#

#dy/dx(x^2-7x+9)=2x-7#

Plug in #x=-1#

#2(-1)-7=-9#

This is our gradient #m=-9#

We need the corresponding #y# value when #x=-1#. Using #f(x)#

#y=((-1)-3)^2-(-1)=17#

Using point slope form of a line:

#(y_2-y_1)=m(x_2-x_1)#

#y-17=-9(x-(-1))#

#color(blue)(y=-9x+8)#

GRAPH:

enter image source here