#f(x)=(2x-1)/e^x# at #x=1/2#
Solve for the point #(x_1, y_1)#
let #x_1=1/2#
#y_1=f(x_1)=(2x_1-1)/e^(x_1)#
#y_1=f(1/2)=(2(1/2)-1)/e^(1/2)#
#y_1=f(1/2)=(1-1)/e^(1/2)=0#
#y_1=0#
Our point #(x_1, y_1)=(1/2, 0)#
Solve for the slope #m#
#f(x)=(2x-1)/e^x#
#f' (x)=(e^x*d/dx(2x-1)-(2x-1)*d/dx(e^x))/(e^x)^2#
#f' (x)=((e^x*2)-(2x-1)*(e^x))/(e^x)^2#
#f' (x)=((2e^x-2xe^x+e^x))/(e^x)^2#
Slope #m=f' (1/2)=((2e^(1/2)-2(1/2)e^(1/2)+e^(1/2)))/(e^(1/2))^2#
#m=f' (1/2)=((2e^(1/2)-e^(1/2)+e^(1/2)))/(e)#
#m=f' (1/2)=(2e^(-1/2))#
For the perpendicular line we need
#m_p=-1/m=-1/((2e^(-1/2))#
#m_p=-1/2e^(1/2)#
Solve for the equation of the line using #color(blue)("Point-Slope Form")#
#y-y_1=m_p(x-x_1)#
#y-0=-1/2e^(1/2)(x-1/2)#
#color(red)(y=-1/2e^(1/2)(x-1/2))#
Kindly see the graph of #f(x)=(2x-1)/e^x# (colored red) and the normal line #y=-1/2e^(1/2)(x-1/2)# (colored blue)
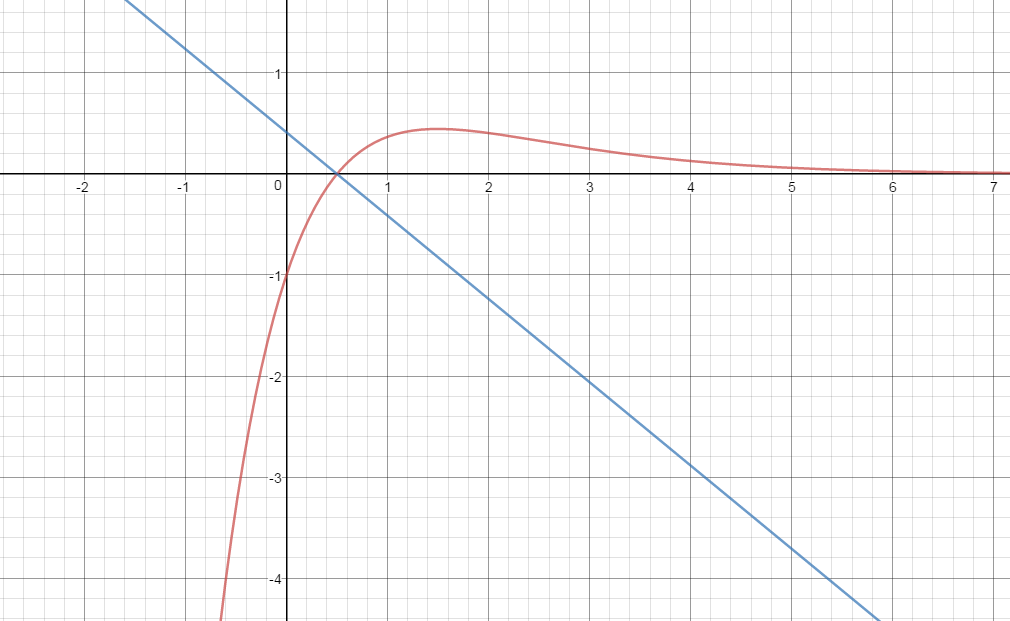
God bless....I hope the explanation is useful.

