What is the equation of the line that is normal to f(x)=e^xcos^2x -xsinx at x=-pi/3?
1 Answer
As a decimal expansion, here's the equation for the normal line to this graph:
y = - .5614x-1.40707
Explanation:
Ok, so I will do almost everything internal to the TI89 and insert jpeg screenshots. This saves me LOTS of time in terms of typing proper syntax using Socratic's proprietary platform.
Here is your equation:
So the first thing is to find f'(x).
This gives what? It gives you the slope of the tangent line to any point on the graph of y = f(x).
Let's call the slope of the tangent line =
You will use the chain rule, product rule, etc.
So....
f'(x) =
Next, what's the point we're talking about here?
Well, it's
Here is a screenshot for

So your equation for the tangent line, using point - slope form and expanding as a decimal approximation gives:
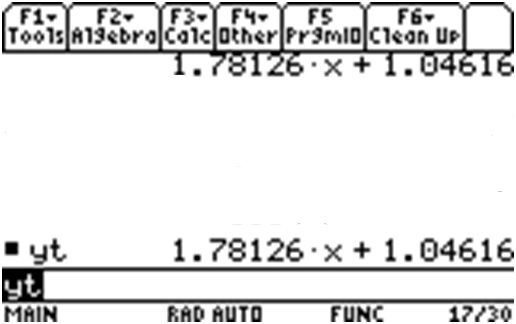
Next. using the negative reciprocal of
Firstly, here's


Here's
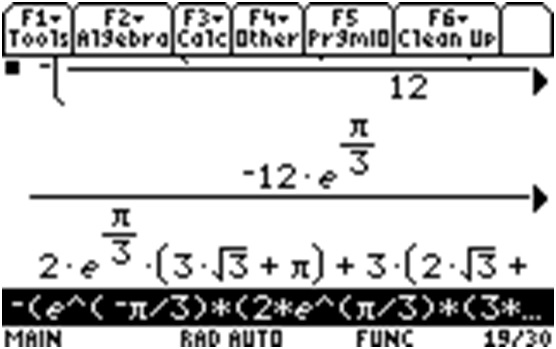
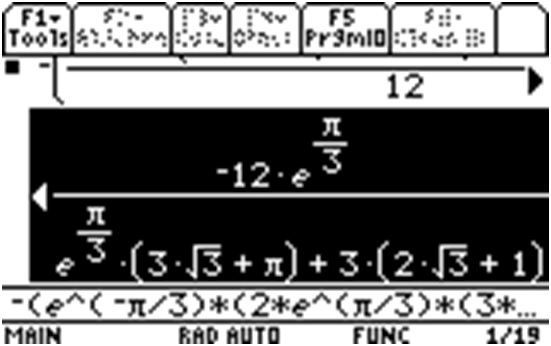
So, once again expressing as a decimal expansion and using the point-slope formula for a line, here's the equation for the normal line:
You need to fill in some of the intermediate algebraic steps.
That's definitely your job. Show all work in terms of finding the derivative using the chain rule and product rule, crunching numbers for respective slopes and arriving at those algebraic expressions for both the tangent line and the normal line.
Keep in mind again that these two lines are by definition, perpendicular.
Finally, here's a pretty picture to confirm all results. Here you see the function f(x) graphed in red, along with both the tangent line and the normal line intersecting at
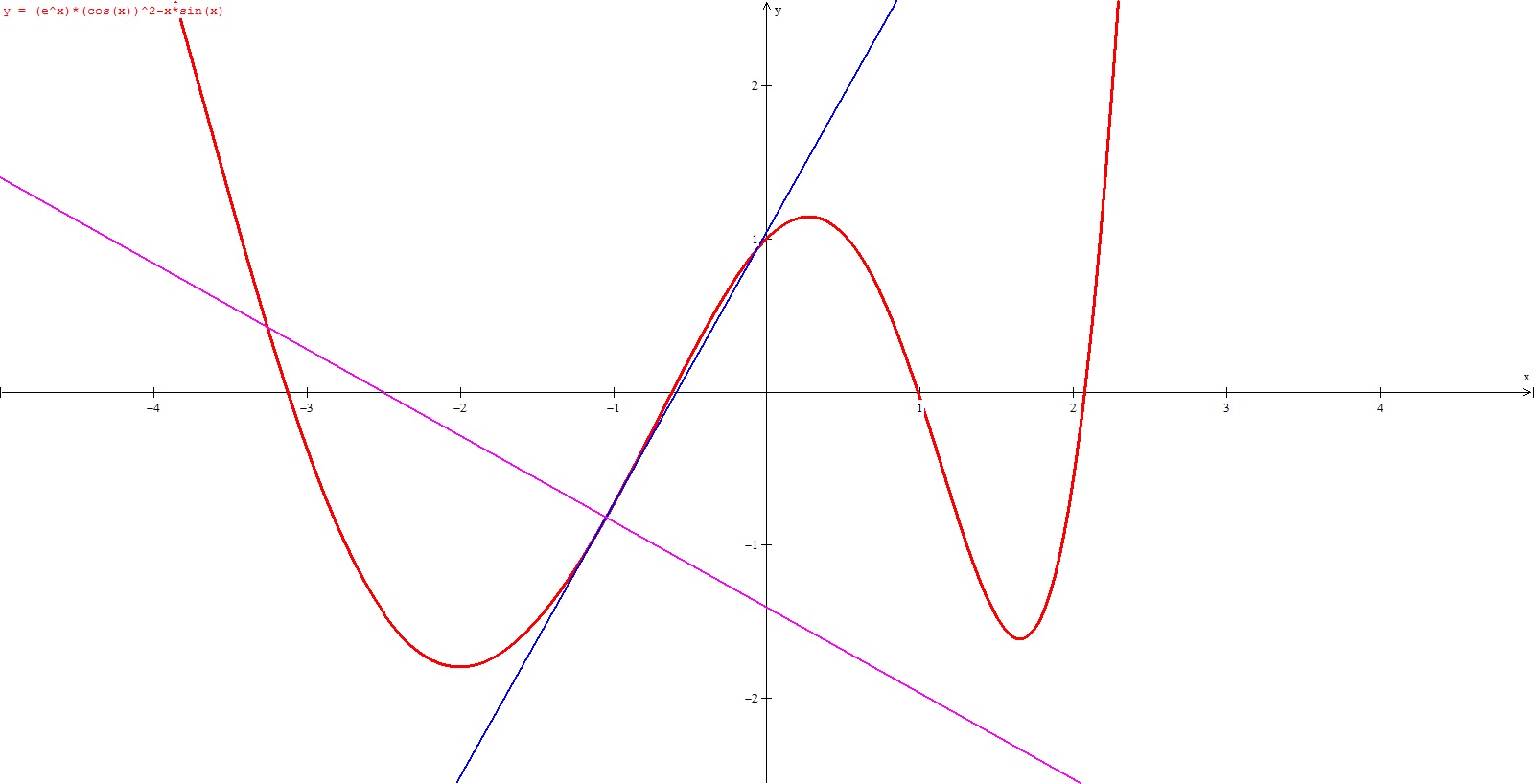
I must now sleep or play guitar or play guitar then sleep.

