Given
#f(x)=tan x-sin 2x# at #x_1=(4pi)/3#
Solve for the point #(x_1, y_1)# first
#y_1=tan x_1-sin 2*x_1#
#y_1=tan ((4pi)/3)-sin (2*(4pi)/3)#
#y_1=sqrt3-sqrt3/2#
#y_1=sqrt3/2#
Our point #(x_1, y_1)=((4pi)/3, sqrt3/2)#
Solve for the slope #m#
#f(x)=tan x-sin 2x#
find the first derivative #f' (x)=m#
#f' (x)=sec^2 x- 2*cos 2x#
#m=f' ((4pi)/3)=sec^2 ((4pi)/3)- 2*cos (2((4pi)/3))#
#m=(-2)^2-2(-1/2)#
#m=4+1=5#
For the normal line
#m_n=-1/m#
#m_n=-1/5#
Solve for the normal line:
#y-y_1=m_n(x-x_1)#
#y-sqrt3/2=-1/5(x-(4pi)/3)#
#y-sqrt3/2=-1/5x+(4pi)/15#
#color(blue)(y=-1/5x+(4pi)/15+sqrt3/2)#
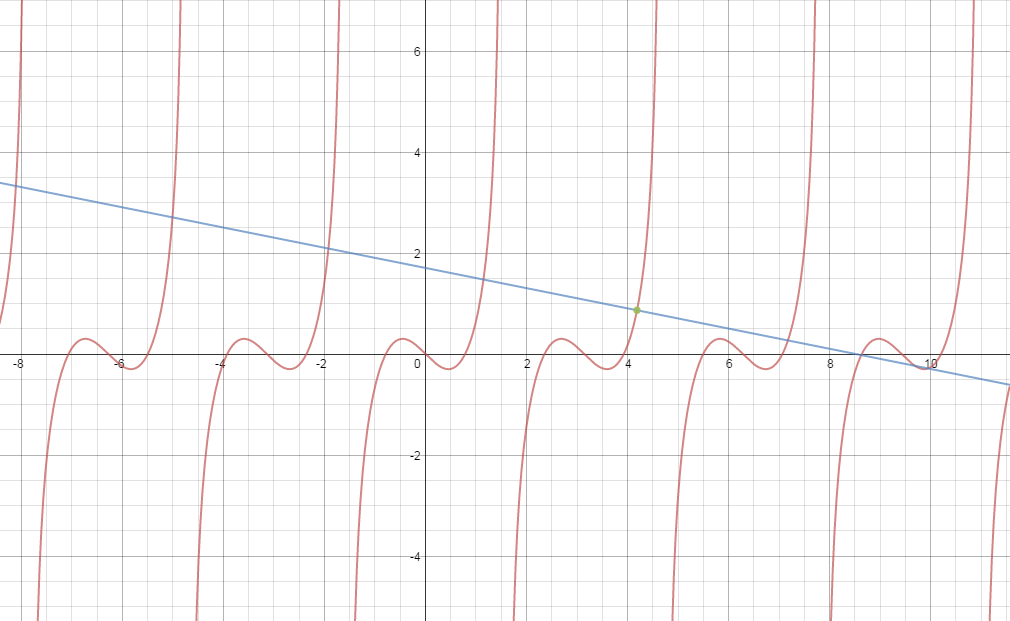
Kindly see the graph of #f(x)=tan x-sin 2x# and the normal line #y=-1/5x+(4pi)/15+sqrt3/2# at the point #((4pi)/3, sqrt3/2)#
God bless....I hope the explanation is useful.

