Question

What is the equation of the line that is normal to `f(x)= (x+2)^2-2x^2+2` at `x=-1`?

Answer 1

`y = -1/6x+5/6`

Explanation:

The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. (If needed, then the normal is perpendicular to the tangent so the product of their gradients is `-1`).

We have:

`f(x) = (x+2)^2-2x^2+2`
`" " = x^2+4x+4-2x^2+2`
`" " = -x^2+4x+6`

Differentiating wrt `x` we have:

`dy/(dx) = -2x+4`

So when `x=-1` we have;

`y = -1-4+6=1` and `dy/dx=2+4=6`

So the tangent/normal passes through `(-1,1)` and has gradient `m_T=6`, so the normal has gradient `m_n=-1/5` and using the point/slope form `y-y_1=m(x-x_1)` the normal equation we seek is;

`y - 1 = -1/6(x+1)`
`y - 1 = -1/6x-1/6`
`y = -1/6x+5/6`

We can verify this graphically:

Answer 2

`y=-1/6x+5/6`

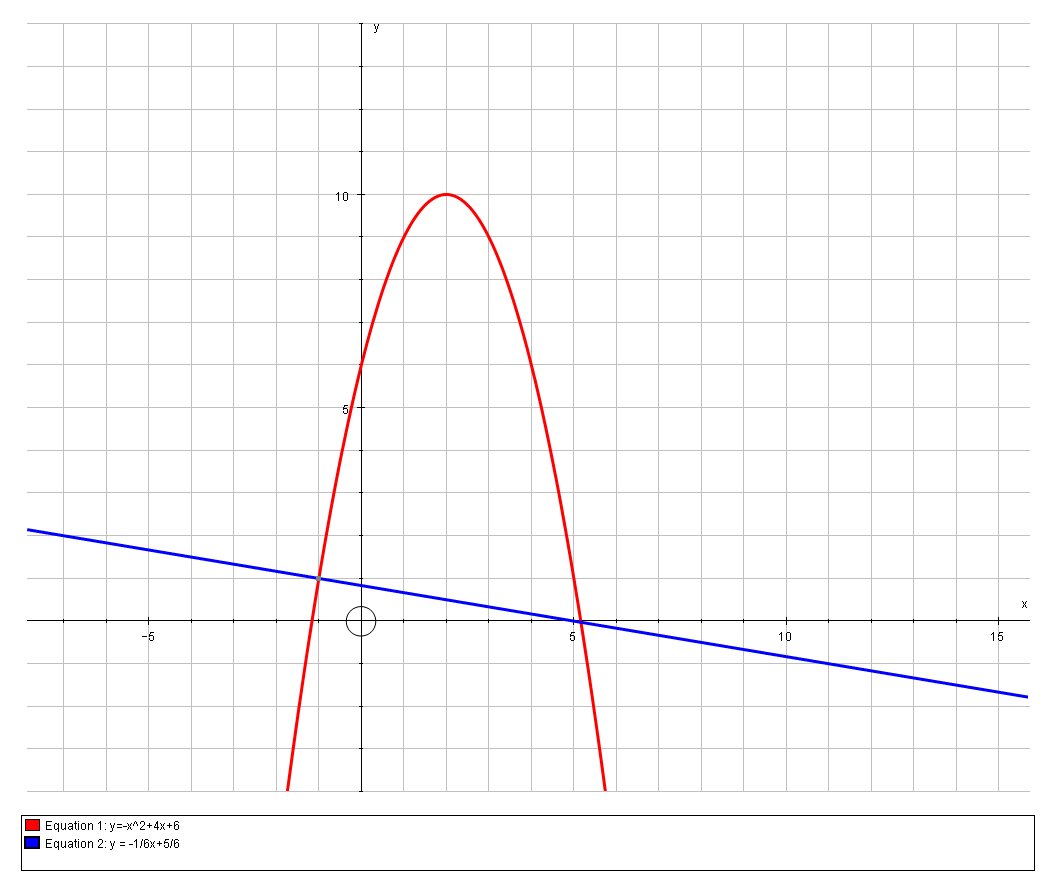
Explanation:

One way to think of the derivative is as a "slope-finding-formula". The result of a derivative is a function, such that when you plug in values for `x`, you find the slope, `m`, of the original function at that point. The line with that slope through that point is called the tangent line.

The normal line is just the perpendicular line through the tangent line, at the same point. Recall from algebra that if you have a slope `m`, the perpendicular slope is

Perpendicular slope: `-1/m`

First, determine the exact point where your normal line will pass through the given curve. This happens at `x=-1`.

`f(-1)=(-1+2)^2-2(-1)^2+2=1`

The point that our normal line will go through is `(-1,1)`

Second, find the derivative, or slope-finding formula. It may help to fully expand out the original function first.

`f(x) = (x+2)^2-2x^2+2`

`f(x)=x^2+4x+4-2x^2+2`

`f(x)=-x^2+4x+6`

Then find the derivative

`f'(x)=-2x+4`

The slope of the tangent line at `x=-1` is

`m=f'(-1)=-2(-1)+4=6`

Therefore, the slope of the perpendicular normal line is

`m_"normal"=-1/m=-1/6`

Now you have all the parts you need to determine the formula for this normal line. You have a slope, `m_"normal"=-1//6` and you have a point through which it travels, `(-1,1)`. Using the point-slope form of a line,

`y-y_1=m_"normal"(x-x_1)`

`y-1=-1/6(x-(-1))`

`y-1=-1/6x-1/6`

`y=-1/6x+5/6`