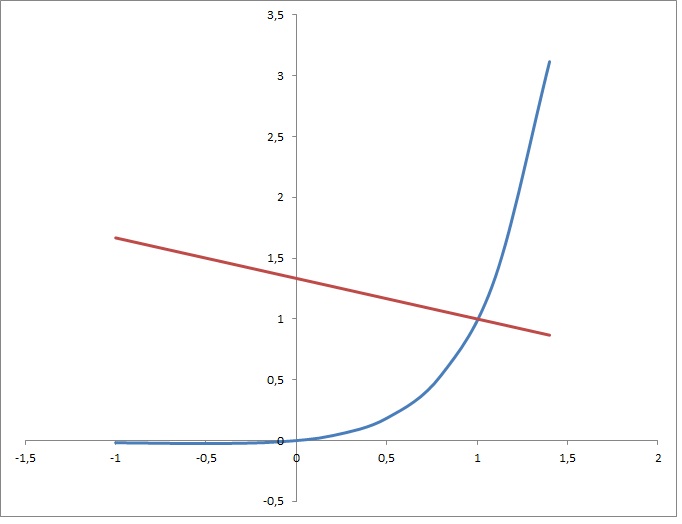
What is the equation of the line that is normal to #f(x)= xe^(2x-2) # at # x= 1 #?
1 Answer
May 18, 2016
I found:
Explanation:
We can first find the coordinates of the point of intersection: knowing that
So we get
Next we try to evaluate the GRADIENT of the line perpendicular (normal).
We evaluate the derivative of the function:
Evaluate the derivative at
This is the slope
Finally we use the general equation of a line through a point and having slope equal to
Graphically: