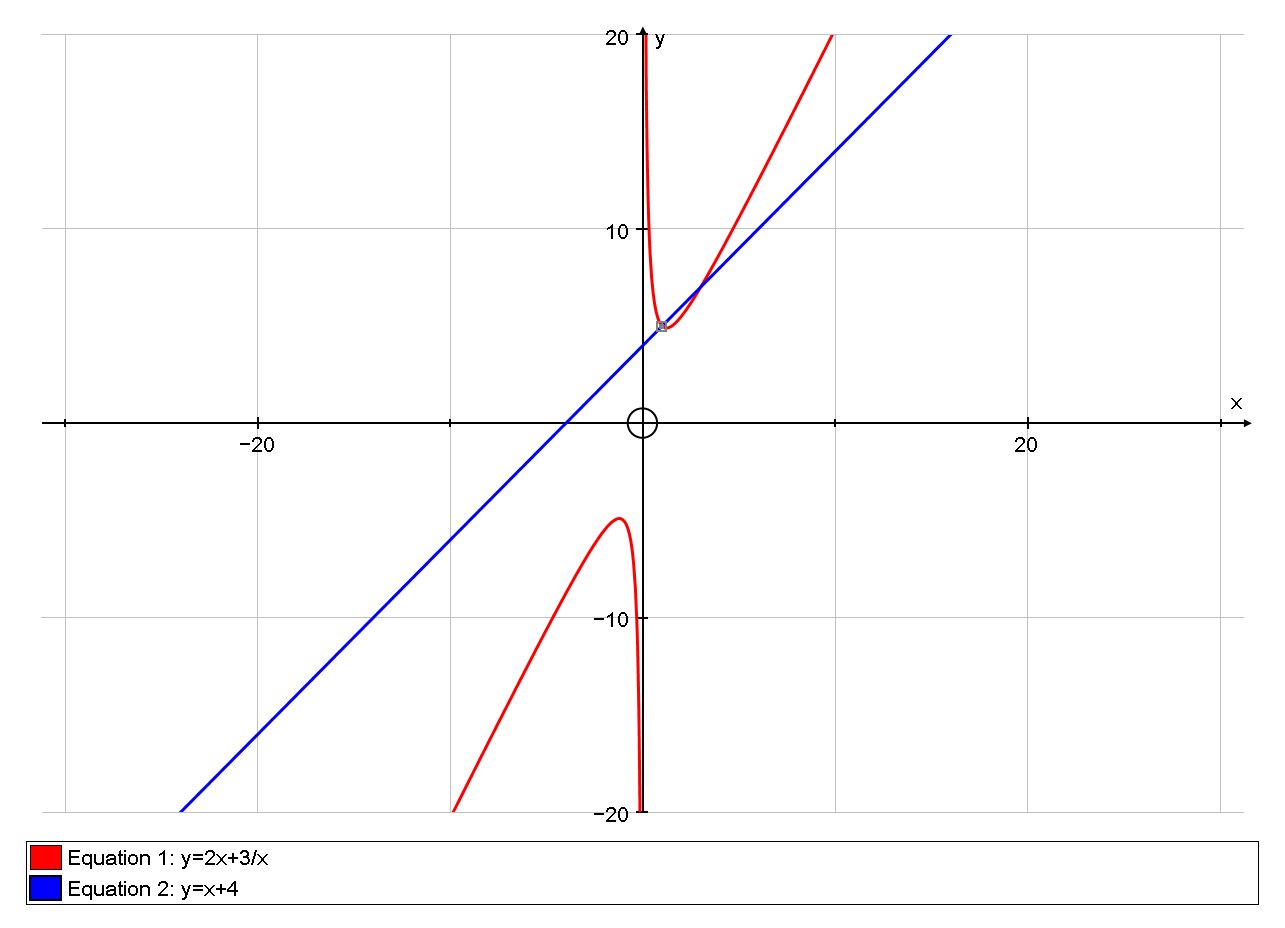
What is the equation of the normal line of #f(x)=2x+3/x# at #x=1#?
1 Answer
Oct 31, 2016
Explanation:
Differentiating wrt
When
and,
So the gradient of the tangent at
Hence, gradient of Normal is
So the Normal has gradient