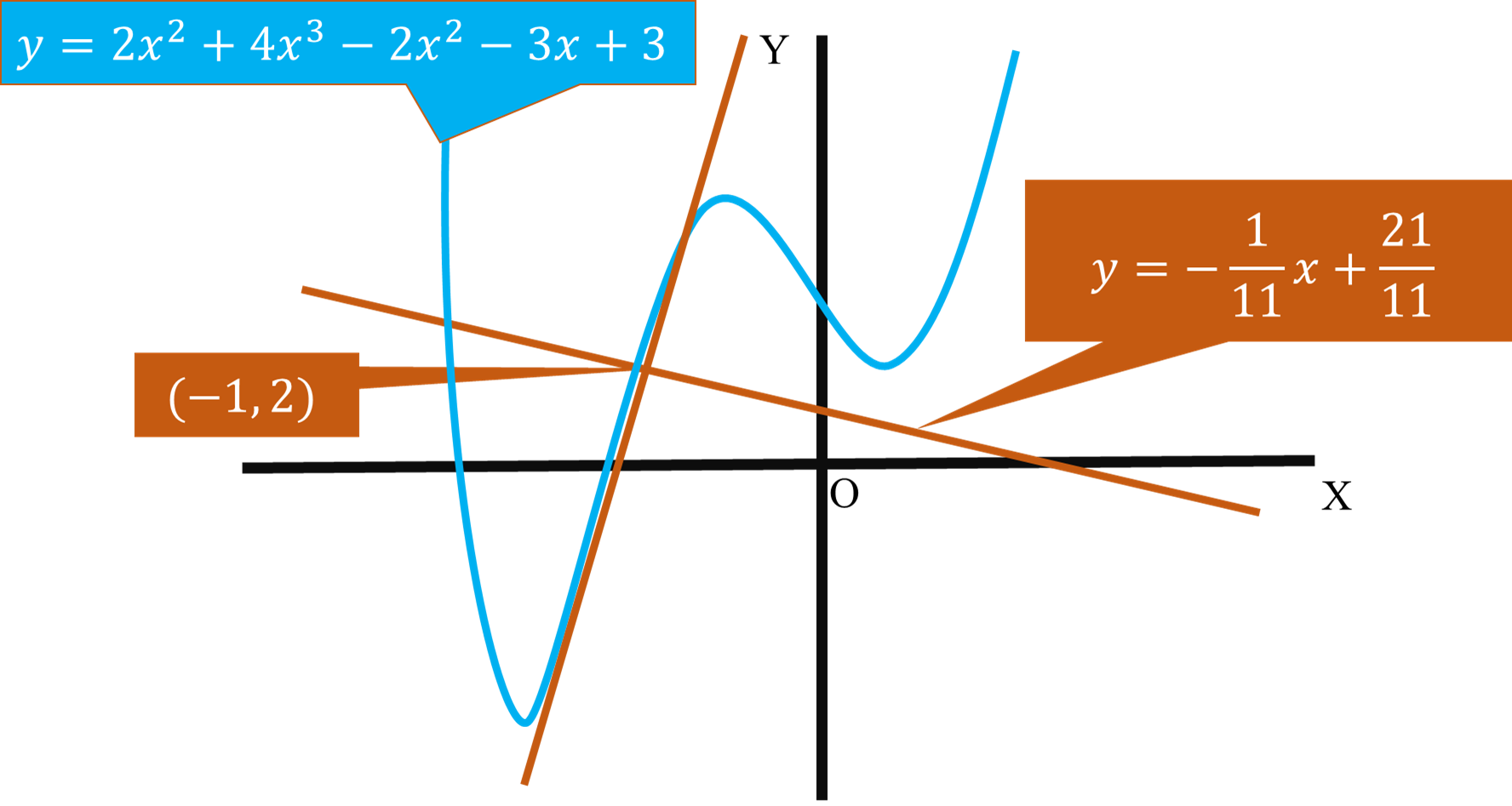
What is the equation of the normal line of #f(x)=2x^4+4x^3-2x^2-3x+3# at #x=-1#?
1 Answer
Aug 27, 2016
#y=-1/11x+21/11#
Explanation:
Given -
#y=2x^4+4x^3-2x^2-3x+3#
The first derivative gives the slope of the curve at any given point.
#dy/dx=8x^3+12x^2_4x-3#
Slope of the curve exactly at
#m_1=8(-1)^3+12(-1)^2-4(-1)+3#
#m_1=-8+12+4+3=11#
This is the slope of the tangent also.
Normal cuts the tangent vertically.
So its slope is
#m_2=-1/11# [Since;# m_1 xx m_2=-1# ]
The normal passes through
Find the Y-coordinate
#y=2(-1)^4+4(-1)^3-2(-1)^2-3(-1)+3#
#y=2-4-2+3+3=2#
The Normal passes through the point
Then find the equation of the Normal
#mx+c=y#
#(-1/11)(-1)+c=2#
#1/11+c=2#
#c=2-1/11=21/11#
The equation of the Normal is-
#y=-1/11x+21/11#