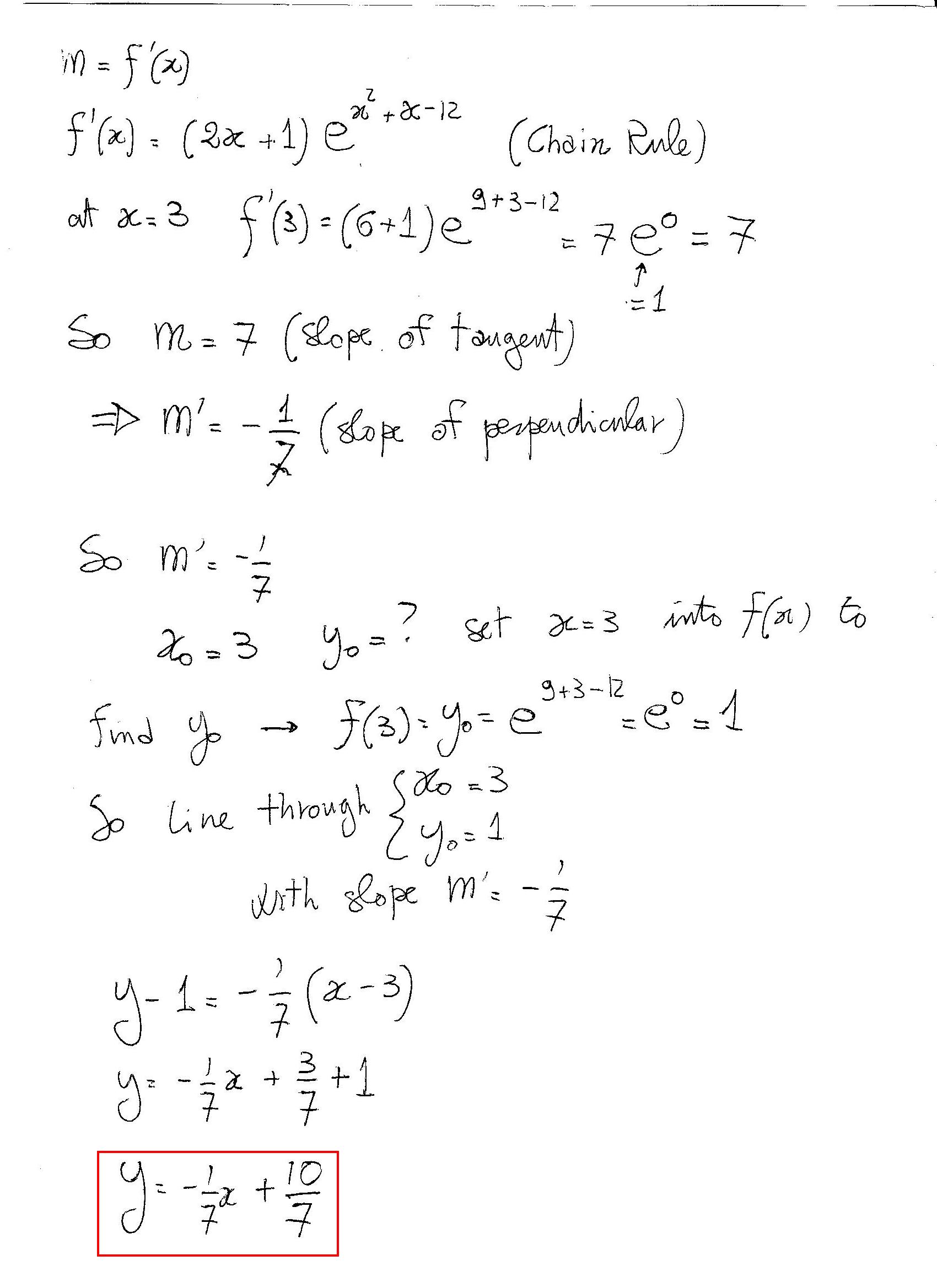What is the equation of the normal line of #f(x)= e^(x^2+x-12)# at #x = 3#?
1 Answer
Dec 20, 2015
I found:
Explanation:
Here I would first find the slope
Then I would evaluate the slope
Finally I would use the relationship:
So: