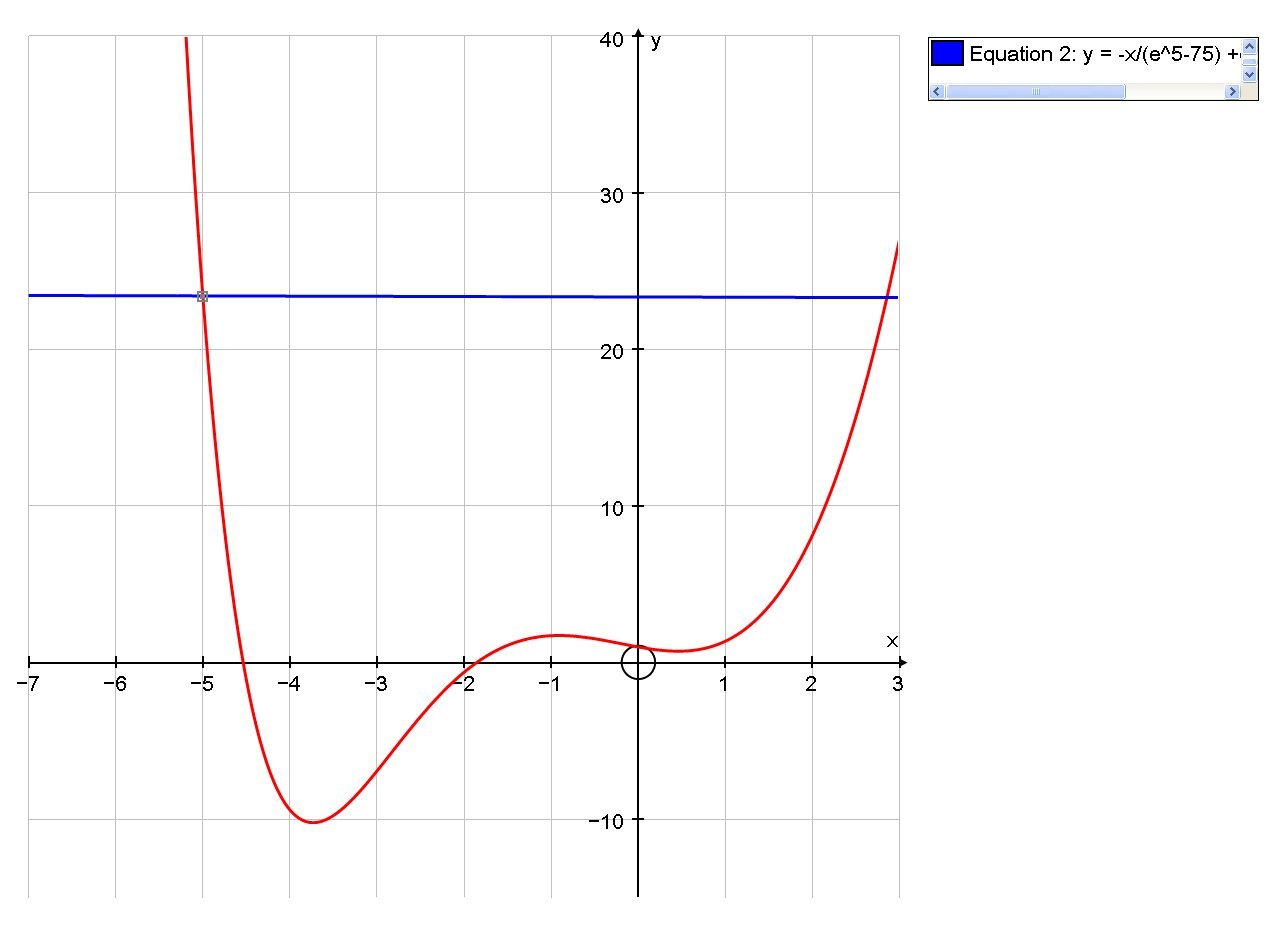
What is the equation of the normal line of #f(x)=e^-x+x^3# at #x=-5#?
1 Answer
Oct 31, 2016
Explanation:
When
Differentiating wrt
so When
This is the slope of the tangent when
So, the slope of the normal is
Using