What is the equation of the normal line of #f(x)=(x-1)(x-3)(x+2) # at #x=3 #?
1 Answer
Dec 18, 2015
Explanation:
Given:
So the point of intersection is going to be at
Expanding the given equation we get
So
And at
Therefore the slope of the normal will be
Using the slope-point form for the normal we have
which can be simplified as
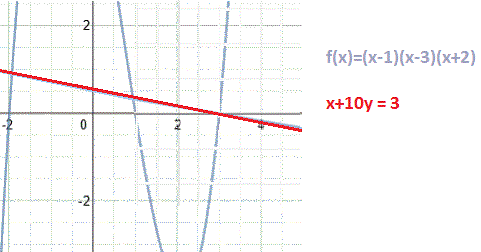
(Sorry about the image quality. I've been having trouble with the graph method and this is an attempt to overlay 2 separate graphs snipped from the screen).
