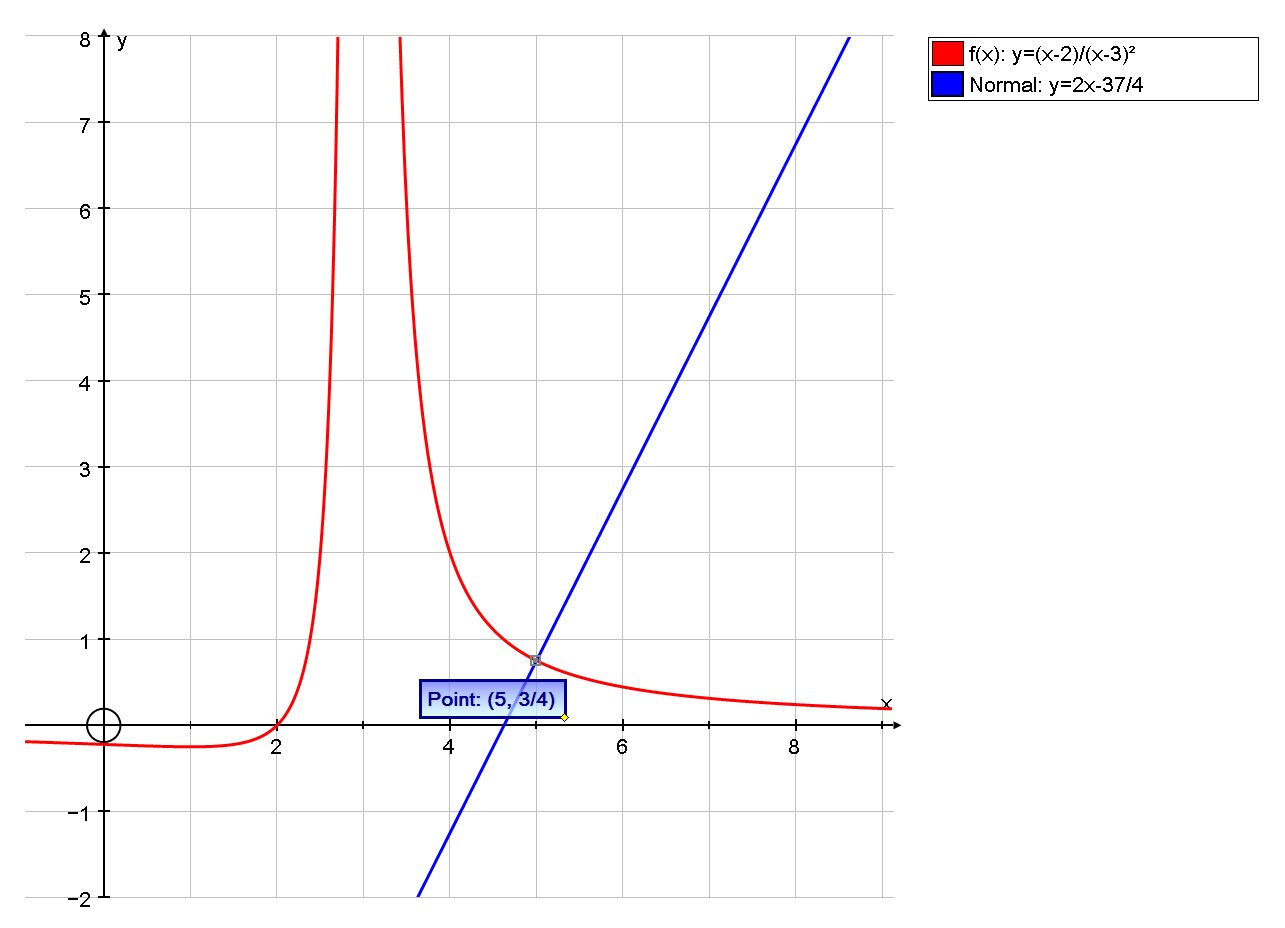
What is the equation of the normal line of #f(x)=(x-2)/(x-3)^2# at #x=5#?
1 Answer
# y=2x-37/4#
Explanation:
We have
Using the quotient rule we have:
# f'(x) = { (x-3)^2 d/dx(x-2) - (x-2)d/dx(x-3)^2 }/ ((x-3)^2)^2#
# :. f'(x) = { (x-3)^2 (1) - (x-2)2(x-3)(1) }/ ((x-3)^4)#
# :. f'(x) = { (x-3){ (x-3) - 2(x-2)} }/ ((x-3)^4)#
# :. f'(x) = { (x-3 - 2x+4) }/ ((x-3)^3)#
# :. f'(x) =(1-x)/ ((x-3)^3)#
When
So the gradient of the tangent when
The tangent and normal are perpendicular so the product of their gradients is
So the gradient of the normal when
Also
So the normal passes through (5,3/4) and has gradient
# y-3/4=2(x-5)#
# y-3/4=2x-10#
# y=2x-37/4#